
如圖,公園有一塊邊長為2的等邊△ABC的邊角地,現修成草坪, 圖中DE把草坪分成面積相等的兩部分,D在AB上,E在AC上.
(1)設 (x≥0),
(x≥0), ,求用
,求用 表示
表示 的函數關系式,并求函數的定義域;
的函數關系式,并求函數的定義域;
(2).如果 是灌溉水管,為節約成本,希望它最短,
是灌溉水管,為節約成本,希望它最短, 的位置應在哪里?如果
的位置應在哪里?如果 是參觀線路,則希望它最長,
是參觀線路,則希望它最長, 的位置又應在哪里?請予證明.
的位置又應在哪里?請予證明.
(1) 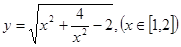
(2) 如果 是水管,當
是水管,當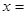
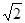 時,
時, 
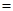
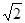 最短.
最短.
如果 是參觀線路,則
是參觀線路,則 為
為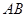 中線或
中線或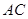 中線時,
中線時, 最長
最長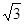 .
.
解析試題分析:(1)顯然變量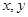 都在
都在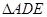 中,尋找兩邊的關系,利用余弦定理即可.但是發現還有邊
中,尋找兩邊的關系,利用余弦定理即可.但是發現還有邊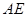 存在,所以得尋找
存在,所以得尋找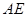 .根據面積相等,利用面積公式即可得到
.根據面積相等,利用面積公式即可得到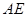 與
與 的關系.消掉
的關系.消掉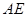 即可得到解析式.但是要考慮實際意義,即函數的定義域.
即可得到解析式.但是要考慮實際意義,即函數的定義域.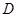 在
在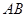 上,可知自變量的范圍是
上,可知自變量的范圍是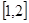 .
.
(2) 如果 是水管,根據(1)中的解析式,觀察形式,可知利用均值不等式即可求得最小值.
是水管,根據(1)中的解析式,觀察形式,可知利用均值不等式即可求得最小值.
如果 是參觀線路,則要求其盡可能的長,所以分析函數的單調性求最大值即可.
是參觀線路,則要求其盡可能的長,所以分析函數的單調性求最大值即可.
(1)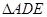 中,根據余弦定理有
中,根據余弦定理有
即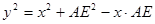 ; ①
; ①
又 ,即
,即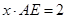 .②
.②
②代入①得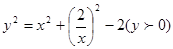 , ∴
, ∴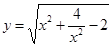
由題意知點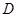 至少是
至少是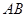 的中點,
的中點, 才能把草坪分成面積相等的兩部分。
才能把草坪分成面積相等的兩部分。
所以 ,又
,又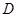 在
在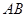 上,
上,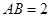 ,所以函數的定義域是
,所以函數的定義域是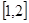 ,
,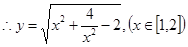 .
.
(2)如果 是水管
是水管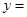
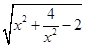
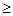
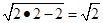 ,
,
當且僅當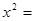
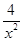 ,即
,即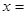
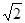 時“=”成立,故
時“=”成立,故 ∥
∥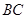 ,且
,且
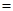
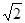 .
.
如果 是參觀線路,記
是參觀線路,記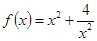 ,可知
,可知
函數在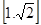 上遞減,在
上遞減,在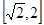 上遞增,
上遞增,
故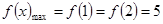 所以
所以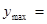
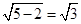 .
.
即 為
為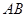 中線或
中線或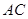 中線時,
中線時, 最長。
最長。
考點:實際應用題;余弦定理;利用均值不等式求函數的最小值;利用函數的單調性得函數的最大值.


 開心試卷期末沖刺100分系列答案
開心試卷期末沖刺100分系列答案 雙基同步導航訓練系列答案
雙基同步導航訓練系列答案科目:高中數學 來源: 題型:解答題
在△ABC中,內角A,B,C所對的邊分別為a,b,c,已知sin B(tan A+tan C)=tan Atan C.
(1)求證:a,b,c成等比數列;
(2)若a=1,c=2,求△ABC的面積S.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
△ABC中,a、b、c分別是角A、B、C的對邊,△ABC的周長為 +2,且sinA+sinB=
+2,且sinA+sinB= sinC.(1)求邊c的長. (2)若△ABC的面積為
sinC.(1)求邊c的長. (2)若△ABC的面積為 sinC,求角C的度數.
sinC,求角C的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com