
已知圓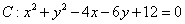 ,
點
,
點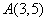 ,
,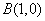 ,求;
,求;
(1)過點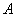 的圓C的切線方程;
的圓C的切線方程;
(2)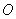 點是坐標原點,連結
點是坐標原點,連結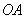 ,
,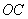 ,求
,求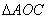 的面積
的面積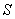 .
.
(3)設動圓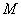 過點
過點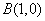 ,且圓心
,且圓心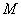 在拋物線
在拋物線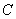 :
: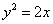 上,
上,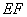 是圓
是圓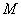 在
在 軸上截得的弦,當
軸上截得的弦,當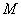 運動時弦長
運動時弦長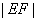 是否為定值?請說明理由.
是否為定值?請說明理由.
 精英口算卡系列答案
精英口算卡系列答案科目:高中數學 來源: 題型:
(本小題滿分15分)已知圓![]() ,點
,點![]() ,直線
,直線![]() .
.
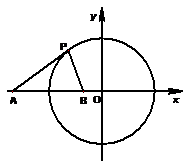 ⑴求與圓
⑴求與圓![]() 相切,且與直線
相切,且與直線![]() 垂直的直線方程;ks5u⑵在直線
垂直的直線方程;ks5u⑵在直線![]() 上(
上(![]() 為坐標原點),存在定點
為坐標原點),存在定點![]() (不同于點
(不同于點![]() ),滿足:對于圓
),滿足:對于圓![]() 上任一點
上任一點![]() ,都有
,都有![]() 為一常數,試求所有滿足條件的點
為一常數,試求所有滿足條件的點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
已知圓![]() ,點
,點![]() ,直線
,直線![]() .
.
⑴求與圓![]() 相切,且與直線
相切,且與直線![]() 垂直的直線方程;ks5u
垂直的直線方程;ks5u
⑵在直線![]() 上(
上(![]() 為坐標原點),存在定點
為坐標原點),存在定點![]() (不同于點
(不同于點![]() ),滿足:對于圓
),滿足:對于圓![]() 上任一點
上任一點![]() ,都有
,都有![]() 為一常數,試求所有滿足條件的點
為一常數,試求所有滿足條件的點![]() 的坐標.
的坐標.
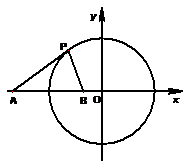
查看答案和解析>>
科目:高中數學 來源: 題型:
(本題滿分14分)已知圓![]() , 點
, 點![]() ,
,![]() ,求;
,求;
(1)過點![]() 的圓C的切線方程; (2)
的圓C的切線方程; (2)![]() 點是坐標原點,連結
點是坐標原點,連結![]() ,
,![]() ,求
,求![]() 的面積
的面積![]() .(3)設動圓
.(3)設動圓![]() 過點
過點![]() ,且圓心
,且圓心![]() 在拋物線
在拋物線![]() :
:![]() 上,
上,![]() 是圓
是圓![]() 在
在![]() 軸上截得的弦,當
軸上截得的弦,當![]() 運動時弦長
運動時弦長![]() 是否為定值?請說明理由.
是否為定值?請說明理由.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年江蘇省高三上學期9月質量檢測數學卷 題型:解答題
(本題滿分16分)
已知圓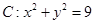 ,點
,點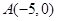 ,直線
,直線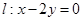 .
.
⑴求與圓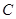 相切,且與直線
相切,且與直線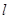 垂直的直線方程;
垂直的直線方程;
⑵在直線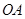 上(
上(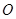 為坐標原點),存在定點
為坐標原點),存在定點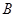 (不同于點
(不同于點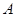 ),滿足:對于圓
),滿足:對于圓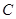 上任一點
上任一點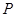 ,都有
,都有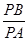 為一常數,試求所有滿足條件的點
為一常數,試求所有滿足條件的點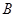 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com