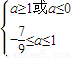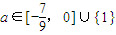命題甲:a∈R,關于x的方程|x|=ax+1(a>0)有兩個非零實數解;
命題乙:a∈R,關于x的不等式(a2-1)x2+(a-1)x-2>0的解集為空集;
當甲、乙中有且僅有一個為真命題時,求實數a的取值范圍.
【答案】
分析:利用圖象法,我們求出函數y=|x|和y=ax+1圖象有兩個交點時,即命題甲為真命題時,實數a的取值范圍,根據一元二次不等式恒成立的充要條件,我們可以求出命題乙為真命題時,實數a的取值范圍,進而根據甲、乙中有且僅有一個為真命題,分類討論后,綜合討論結果,即可得到答案.
解答:解:當甲真時,設y=|x|和y=ax+1(a>0),即兩函數圖象有兩個交點.
則0<a<1
當乙真時,不等式(a
2-1)x
2+(a-1)x-2>0的解集為空集,;①a
2-1=0且a-1=0,得:a=1時 滿足題意,
②a
2-1<0且△≤0,即
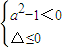
也滿足
則
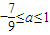
∴當甲乙有但僅有一個為真命題時,即
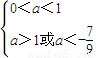
或
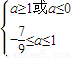
∴
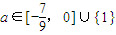 點評:
點評:本題考查的知識點是命題的真假判斷與應用,其中利用圖象法,求出命題甲為真命題時,實數a的取值范圍,根據一元二次不等式恒成立的充要條件,求出命題乙為真命題時,實數a的取值范圍,是解答本題的關鍵.

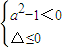 也滿足
也滿足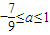
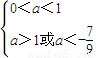 或
或