
正方體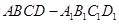 的棱線長為1,面對角線
的棱線長為1,面對角線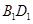 上有兩個動點E,F,且
上有兩個動點E,F,且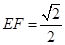 ,則下列四個結論中①
,則下列四個結論中①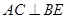 ②
②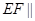 平面
平面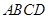 ③三棱錐
③三棱錐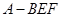 的體積為定值 ④異面直線
的體積為定值 ④異面直線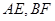 所成的角為定值,其中正確的個數是
所成的角為定值,其中正確的個數是
| A.1 | B.2 | C.3 | D.4 |
C
解析試題分析:①AC⊥BE,由題意及圖形知,AC⊥面DD1B1B,故可得出AC⊥BE,此命題正確;
②EF∥平面ABCD,由正方體ABCD-A1B1C1D1的兩個底面平行,EF在其一面上,故EF與平面ABCD無公共點,故有EF∥平面ABCD,此命題正確;
③三棱錐A-BEF的體積為定值,由幾何體的性質及圖形知,三角形BEF的面積是定值,A點到面DD1B1B距離是定值,故可得三棱錐A-BEF的體積為定值,此命題正確;
④異面直線AE、BF所成的角為定值,由圖知,當F與B1重合時,令上底面頂點為O,則此時兩異面直線所成的角是∠A1AO,當E與D1重合時,此時點F與O重合,則兩異面直線所成的角是OBC1,此二角不相等,故異面直線AE、BF所成的角不為定值.
綜上知①②③正確,故選C。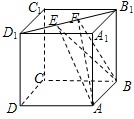
考點:本題主要考查正方體的幾何性質。
點評:中檔題,解答本題關鍵是正確理解正方體的幾何性質,且能根據這些幾何特征,對其中的點線面和位置關系作出正確判斷.另外,異面直線所成角的定義以及線面垂直的證明也是解答本題的關鍵。


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:單選題
下面四個命題:
①若直線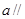 平面
平面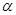 ,則
,則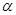 內任何直線都與
內任何直線都與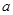 平行;
平行;
②若直線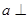 平面
平面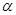 ,則
,則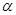 內任何直線都與
內任何直線都與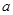 垂直;
垂直;
③若平面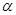
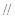 平面
平面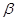 ,則
,則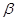 內任何直線都與
內任何直線都與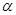 平行;
平行;
④若平面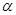
 平面
平面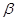 ,則
,則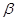 內任何直線都與
內任何直線都與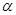 垂直。
垂直。
其中正確的兩個命題是( )
| A.①② | B.②③ | C.③④ | D.②④ |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
若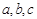 是空間三條不同的直線,
是空間三條不同的直線,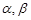 是空間兩個不同的平面,則下列命題中,逆命題不正確的是( )
是空間兩個不同的平面,則下列命題中,逆命題不正確的是( )
A.當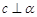 時,若 時,若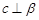 ,則 ,則 |
B.當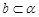 時,若 時,若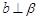 ,則 ,則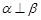 |
C.當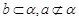 且 且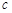 是 是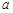 在 在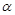 內的射影時,若 內的射影時,若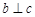 ,則 ,則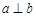 |
D.當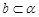 且 且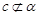 時,若 時,若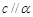 ,則 ,則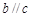 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
在空間,下列命題正確的是( )
| A.平行直線在同一平面內的射影平行或重合 | B.垂直于同一平面的兩條直線平行 |
| C.垂直于同一平面的兩個平面平行 | D.平行于同一直線的兩個平面平行 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
已知m,n為異面直線,m⊥平面α,n⊥平面β,直線l滿足l ⊥m,l ⊥n,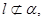 l
l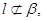 則
則
( )
A.α∥β且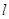 ∥α ∥α | B.α⊥β且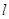 ⊥β ⊥β |
C.α與β相交,且交線垂直于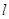 | D.α與β相交,且交線平行于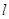 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com