
①f(-1)=f(1)=0;
②對任意u,v∈[-1,1]都有|f(u)-f(v)|≤|u-v|.
(1)證明對任意的x∈[-1,1],都有x-1≤f(x)≤1-x;
(2)證明對任意的u,v∈[-1,1],都有|f(u)-f(v)|≤1;
(3)在區間[-1,1]上是否存在滿足條件的奇函數y=f(x),且使得

若存在,請舉一例;若不存在,請說明理由.
(1)證明:由題設條件可知,當x∈[-1,1],
|f(x)|=|f(x)-f(1)|≤|x-1|=1-x,
即x-1≤f(x)≤1-x.
(2)證明:對任意的u,v∈[-1,1],
當|u-v|≤1時,有|f(u)-f(v)|≤|u-v|≤1.
當|u-v|>1時,有u·v<0.
不妨設u<0,則v>0且v-u>1,
所以|f(u)-f(v)|≤|f(u)-f(-1)|+|f(v)-f(1)|≤|u+1|+|v-1|=1+u+1-v=2-(v-u)<1.
綜上可知,對任意的u,v∈[-1,1],都有|f(u)-f(v)|≤1.
(3)解析:滿足所述條件的函數不存在,理由如下:假設存在函數f(x)滿足條件,
則由|f(u)-f(v)|=|u-v|,u,v∈[![]() ,1]得
,1]得
|f(![]() )-f(1)|=|
)-f(1)|=|![]() -1|=
-1|=![]() .
.
又f(1)=0,所以|f(![]() )|=
)|=![]() .①
.①
又因為f(x)為奇函數,所以f(0)=0.
由條件|f(u)-f(v)|<|u-v|,u,v∈[0,![]() ]得
]得
|f(![]() )|=|f(
)|=|f(![]() )-f(0)|<
)-f(0)|<![]() .②
.②
①與②矛盾,所以假設不成立,即這樣的函數不存在.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:044
設
y=f(x)是定義在區間[-1,1]上的函數,且滿足條件:①f(-1)=f(1)=0;②對任意的u,v∈[-1,1],都有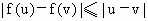 .
.
(1)
證明:對任意的x∈[-1,1],都有x-1≤f(x)≤1-x.(2)
證明:對任意的u,v∈[-1,1],都有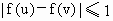 .
.
(3)
在區間[-1,1]上是否存在滿足題設條件的奇函數y=f(x),且使得: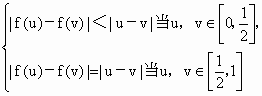
若存在,請舉一例;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:044
①f(-1)=f(1)=0;
②對任意u,v∈[-1,1]都有|f(u)-f(v)|≤|u-v|.
(1)證明對任意的x∈[-1,1],都有x-1≤f(x)≤1-x;
(2)證明對任意的u,v∈[-1,1],都有|f(u)-f(v)|≤1;
(3)在區間[-1,1]上是否存在滿足條件的奇函數y=f(x),且使得

若存在,請舉一例;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源:廣東省模擬題 題型:證明題
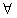 x1、x2∈(a,b),都有|f(x1)-f(x2)|≤|x1-x2|,則稱y=f(x)是區間(a,b)上的平緩函數.
x1、x2∈(a,b),都有|f(x1)-f(x2)|≤|x1-x2|,則稱y=f(x)是區間(a,b)上的平緩函數. 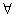 k∈R,f(x)=x2+kx+1都不是區間(-1,1)上的平緩函數;
k∈R,f(x)=x2+kx+1都不是區間(-1,1)上的平緩函數;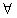 x1、x2∈R,|f(x1)-f(x2)|≤1.
x1、x2∈R,|f(x1)-f(x2)|≤1. 查看答案和解析>>
科目:高中數學 來源: 題型:
(i)f(-1)=f(1)=0;
(ii)對任意的u、v∈[-1,1]都有|f(u)-f(v)|≤|u-v|.
(1)證明對x∈[-1,1]都有x-1≤f(x)≤1-x;
(2)證明對任意的u、v∈[-1,1]都有|f(u)-f(v)|≤1.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com