中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

已知函數.
(1)求函數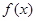的最小正周期和圖像的對稱軸方程；
(2)求函數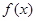在區間上的值域.

（1），；（2） 

解析試題分析：（1）先利用兩角和與差的三角函數將式子展開合并，再利用二倍角公式、輔助角公式化簡得到，再結合正弦函數的性質，由、可得函數的最小正周期與對稱軸的方程；（2）將當成整體，由，利用正弦函數的單調性可得，即的值域.
試題解析：（1）



所以函數的周期
由，得
所以函數圖像的對稱軸方程為  6分
（2）因為，所以
因為在區間上單調遞增，在區間上單調遞減
所以當時，取最大值1
又因為，當時，取最小值
所以函數在區間上的值域為   10分.
考點：1.三角函數的圖像與性質；2.三角恒等變換.

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：解答題

已知f(x)=Asin(ωx+φ)(A>0,ω>0)的最小正周期為2,且當x=時,f(x)的最大值為2.
(1)求f(x)的解析式.
(2)在閉區間[,]上是否存在f(x)的對稱軸?如果存在求出其對稱軸.若不存在,請說明理由.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

已知
（1）求的值；
（2）求的值；
（3）若是第三象限角，求的值.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

已知函數.
（1）請用“五點法”畫出函數在長度為一個周期的閉區間上的簡圖（先在所給的表格中填上所需的數值，再畫圖）；

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

（2）求函數的單調遞增區間；
（3）當時，求函數的最大值和最小值及相應的的值.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

已知函數（其中）的部分圖象如圖所示．

（1）求函數的解析式；
（2）求函數的單調增區間；
（3）求方程的解集．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

已知向量a=，b=，設函數=ab．
（Ⅰ）求的單調遞增區間；
（Ⅱ）若將的圖象向左平移個單位，得到函數的圖象，求函數在區間上的最大值和最小值．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

已知函數．
（Ⅰ）求的值；
（Ⅱ）求在區間上的最大值和最小值．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

在中,已知.
（1）求證:;
（2）若求角A的大小.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

在中,三個內角所對的邊分別為已知，.
（1）求；
（2）設求的值.

查看答案和解析>>

同步練習冊答案