
已知向量a= ,b=
,b= ,設函數
,設函數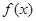 =a
=a b.
b.
(Ⅰ)求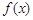 的單調遞增區間;
的單調遞增區間;
(Ⅱ)若將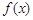 的圖象向左平移
的圖象向左平移 個單位,得到函數
個單位,得到函數 的圖象,求函數
的圖象,求函數 在區間
在區間 上的最大值和最小值.
上的最大值和最小值.
(Ⅰ)f(x)的遞增區間是[- +kπ,
+kπ, +kπ]( k∈Z);(II)最大值為
+kπ]( k∈Z);(II)最大值為 +1,最小值為0.
+1,最小值為0.
解析試題分析:(Ⅰ)將f(x)=a•b=2sin2x+2sinxcosx降次化一,化為 的形式,然后利用正弦函數的單調區間,即可求得其單調遞增區間.(II)將
的形式,然后利用正弦函數的單調區間,即可求得其單調遞增區間.(II)將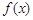 的圖象向左平移
的圖象向左平移 個單位,則將
個單位,則將 換成
換成 得到函數
得到函數 的解析式g(x)=
的解析式g(x)= sin[2(x+
sin[2(x+ )-
)- ]+1=
]+1= sin(2x+
sin(2x+ )+1.由
)+1.由 ≤x≤
≤x≤ 得
得 ≤2x+
≤2x+ ≤
≤ ,結合正弦函數的圖象可得0≤g(x)≤
,結合正弦函數的圖象可得0≤g(x)≤ +1,從而得g(x)的最大值和最小值.
+1,從而得g(x)的最大值和最小值.
試題解析:(Ⅰ)f(x)=a•b=2sin2x+2sinxcosx
= +sin2x
+sin2x
= sin(2x-
sin(2x- )+1, 3分
)+1, 3分
由- +2kπ≤2x-
+2kπ≤2x- ≤
≤ +2kπ,k∈Z,得-
+2kπ,k∈Z,得- +kπ≤x≤
+kπ≤x≤ +kπ,k∈Z,
+kπ,k∈Z,
∴f(x)的遞增區間是[- +kπ,
+kπ, +kπ](k∈Z). 6分
+kπ](k∈Z). 6分
(II)由題意g(x)= sin[2(x+
sin[2(x+ )-
)- ]+1=
]+1= sin(2x+
sin(2x+ )+1, 9分
)+1, 9分
由 ≤x≤
≤x≤ 得
得 ≤2x+
≤2x+ ≤
≤ ,
,
∴ 0≤g(x)≤ +1,即 g(x)的最大值為
+1,即 g(x)的最大值為 +1,g(x)的最小值為0. 12分
+1,g(x)的最小值為0. 12分
考點:1、向量及三角恒等變換;2、三角函數的單調區間及范圍.


 全能練考卷系列答案
全能練考卷系列答案科目:高中數學 來源: 題型:解答題
已知函數f(x)= sin ωx-sin2
sin ωx-sin2 +
+ (ω>0)的最小正周期為π.
(ω>0)的最小正周期為π.
(1)求ω的值及函數f(x)的單調遞增區間;
(2)當x∈ 時,求函數f(x)的取值范圍.
時,求函數f(x)的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數 的周期為
的周期為 .
.
(1)若 ,求它的振幅、初相;
,求它的振幅、初相;
(2)在給定的平面直角坐標系中作出該函數在 的圖像;
的圖像;
(3)當 時,根據實數
時,根據實數 的不同取值,討論函數
的不同取值,討論函數 的零點個數.
的零點個數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com