
已知函數 (a為常數)在x=1處的切線的斜率為1.
(a為常數)在x=1處的切線的斜率為1.
(1)求實數a的值,并求函數 的單調區間,
的單調區間,
(2)若不等式 ≥k在區間
≥k在區間 上恒成立,其中e為自然對數的底數,求實數k的取值范圍.
上恒成立,其中e為自然對數的底數,求實數k的取值范圍.
(1)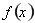 的單調遞增區間是
的單調遞增區間是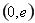 ,
,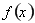 的單調遞減區間是
的單調遞減區間是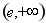 ;(2)
;(2)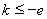 .
.
【解析】
試題分析:(1)先求 ,利用在
,利用在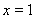 處的導數就是此點處切線斜率,即
處的導數就是此點處切線斜率,即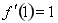 ,算出a,然后確定函數的定義域,利用
,算出a,然后確定函數的定義域,利用 的區間為函數的增區間,
的區間為函數的增區間,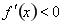 的區間為函數的減區間;(2)將不等式恒成立轉化成
的區間為函數的減區間;(2)將不等式恒成立轉化成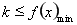 ,利用(1)
,利用(1)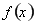 在
在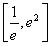 的單調性,判斷出
的單調性,判斷出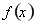 在
在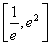 上的最小值為
上的最小值為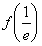 或
或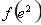 ,所以分別求出
,所以分別求出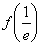 和
和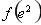 ,然后比較得出最小值.即
,然后比較得出最小值.即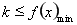 ,此題考察利用導數研究函數性質,邏輯推理要嚴謹,此題屬于中檔題.
,此題考察利用導數研究函數性質,邏輯推理要嚴謹,此題屬于中檔題.
試題解析:(1)
由題知: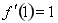 即
即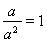 ,解得,
,解得,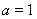 .
.
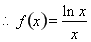 ,定義域
,定義域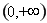
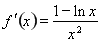 ,由
,由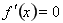 ,得
,得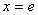 ,
,
當 時,
時,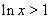 ,此時,
,此時, ,
,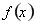 在
在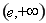 上單調遞減.
上單調遞減.
當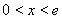 時,
時,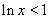 ,此時,
,此時,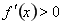 ,
, 在
在 上單調遞增.
上單調遞增.
綜上: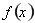 的單調遞增區間是
的單調遞增區間是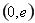 ,
,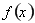 的單調遞減區間是
的單調遞減區間是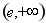 .
.
(2)由(1)知 在上
在上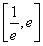 單調遞增,在
單調遞增,在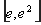 上單調遞減.
上單調遞減.
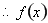 在
在 上的最小值為
上的最小值為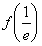 或
或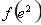
又 ,
,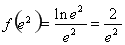 且
且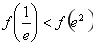
 在
在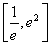 上的最小值為
上的最小值為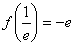
若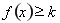 在
在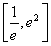 上恒成立,則
上恒成立,則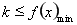
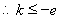
考點:1.求函數的導數;2.利用導數求函數的單調區間和最值.


 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:高中數學 來源:2012年寧夏高考數學仿真模擬試卷3(文科)(解析版) 題型:解答題
 ( a為常數、a∈R),
( a為常數、a∈R), .
.查看答案和解析>>
科目:高中數學 來源:2010年上海市普陀區曹楊二中高考數學模擬試卷(文科)(解析版) 題型:解答題
 (a為常數)的圖象經過點(1,3).
(a為常數)的圖象經過點(1,3).查看答案和解析>>
科目:高中數學 來源:2009-2010學年安徽省皖中地區示范高中高三聯考數學試卷(文科)(解析版) 題型:解答題
 ( a為常數、a∈R),
( a為常數、a∈R), .
.查看答案和解析>>
科目:高中數學 來源:2010年青海省高一上學期期中考試數學試卷 題型:解答題
已知函數 (a為常數)是R上的奇函數,函數
(a為常數)是R上的奇函數,函數
是區間[-1,1]上的減函數.
(1)求a的值;
(2)若 上恒成立,求t的取值范圍
上恒成立,求t的取值范圍
查看答案和解析>>
科目:高中數學 來源:2010年貴州省遵義市高三考前最后一次模擬測試數學(理)試題 題型:解答題
(本小題滿分12分)
已知函數 其中a為常數,且
其中a為常數,且 .
.
(Ⅰ)當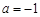 時,求
時,求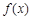 在
在 (e=2.718 28…)上的值域;
(e=2.718 28…)上的值域;
(Ⅱ)若 對任意
對任意 恒成立,求實數a的取值范圍.
恒成立,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com