
解析:解法(一):
![]() 時(shí),
時(shí),![]() 即
即![]() ……①
……①
⑴![]() 時(shí),
時(shí),![]() 恒成立,
恒成立,![]()
⑵![]() 時(shí),①式化為
時(shí),①式化為![]() ……②
……②
⑶![]() 時(shí),①式化為
時(shí),①式化為![]() ……③………………………………………5分
……③………………………………………5分
記![]() ,則
,則![]() ……………7分
……………7分
![]()
![]()
![]()
所以![]()
![]()
故由②![]() ,由③
,由③![]() …………………………………………13分
…………………………………………13分
綜上![]() 時(shí),
時(shí),![]() 在
在![]() 恒成立.………………………………14分
恒成立.………………………………14分
解法(二):
![]() 時(shí),
時(shí),![]() 即
即![]() ……①
……①
⑴![]() 時(shí),
時(shí),![]() ,
,![]() ,不合題意………………………………2分
,不合題意………………………………2分
⑵![]() 恒成立
恒成立
∴![]() 在
在![]() 上為減函數(shù),
上為減函數(shù),![]()
得![]() ,矛盾,…………………………………………………………………5分
,矛盾,…………………………………………………………………5分
⑶![]() ,
,![]() =
=![]()
![]()
若![]() 則
則![]() ,
,![]() ,故在[-1,1]內(nèi),
,故在[-1,1]內(nèi),
![]() ,得
,得![]() ,矛盾.
,矛盾.
若![]()
![]()
依題意,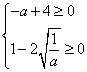 解得
解得![]() 即
即![]()


 沖刺100分1號(hào)卷系列答案
沖刺100分1號(hào)卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:2010年廣東省實(shí)驗(yàn)中學(xué)高二期末測(cè)試數(shù)學(xué)(理) 題型:解答題
(本題滿分14分)設(shè)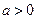 ,函數(shù)
,函數(shù)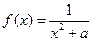 .
.
(Ⅰ)證明:存在唯一實(shí)數(shù)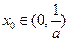 ,使
,使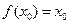 ;
;
(Ⅱ)定 義數(shù)列
義數(shù)列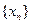 :
: ,
,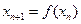 ,
,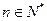 .
.
(i)求證:對(duì)任意正整數(shù)n都有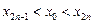 ;
;
(ii) 當(dāng)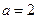 時(shí),若
時(shí),若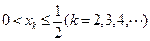 ,
,
證明:當(dāng)k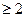 時(shí),對(duì)任意
時(shí),對(duì)任意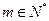 都有:
都有: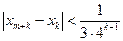
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2015屆廣東始興風(fēng)度中學(xué)高一上期末考試數(shù)學(xué)試卷(解析版) 題型:解答題
(本題14分)設(shè)函數(shù)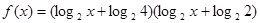 的定義域?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013100823485994997087/SYS201310082349271289438345_ST.files/image002.png">,
的定義域?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013100823485994997087/SYS201310082349271289438345_ST.files/image002.png">,
(Ⅰ)若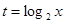 ,求
,求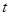 的取值范圍;
的取值范圍;
(Ⅱ)求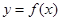 的最大值與最小值,并求出最值時(shí)對(duì)應(yīng)的
的最大值與最小值,并求出最值時(shí)對(duì)應(yīng)的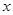 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014屆廣東雷州一中.徐聞中學(xué)高一下學(xué)期第二次聯(lián)考數(shù)學(xué)卷(解析版) 題型:解答題
(本題滿分14分)設(shè)函數(shù)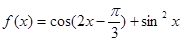 ,
,
(1)求函數(shù) 的最大值和最小正周期;
的最大值和最小正周期;
(2)設(shè) 為
為 的三個(gè)內(nèi)角,若
的三個(gè)內(nèi)角,若 ,且
,且 為銳角,求
為銳角,求 的值。
的值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年廣東省高三上學(xué)期期中考試?yán)砜茢?shù)學(xué)卷 題型:解答題
(本小題滿分14分)
設(shè)函數(shù)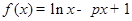
(Ⅰ)研究函數(shù)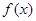 的極值點(diǎn);
的極值點(diǎn);
(Ⅱ)當(dāng)p>0時(shí),若對(duì)任意的x>0,恒有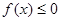 ,求p的取值范圍;
,求p的取值范圍;
(Ⅲ)證明: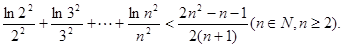
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本小題滿分14分)設(shè)函數(shù)![]() ,若a是從1,2,3三個(gè)數(shù)中任取一個(gè)數(shù),b是從2,3,4,5四個(gè)數(shù)中任取一個(gè)數(shù),(Ⅰ)求f(x)的最小值;(Ⅱ)求f(x)>b恒成立的概率.
,若a是從1,2,3三個(gè)數(shù)中任取一個(gè)數(shù),b是從2,3,4,5四個(gè)數(shù)中任取一個(gè)數(shù),(Ⅰ)求f(x)的最小值;(Ⅱ)求f(x)>b恒成立的概率.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com