如圖，制圖工程師要用兩個同中心的邊長均為4的正方形合成一個八角形圖形．由對稱性，圖中8個三角形都是全等的三角形，設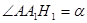
．
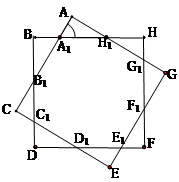
（1）試用
表示
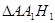的面積；
（2）求八角形所覆蓋面積的最大值，并指出此時的大小．
科目：高中數(shù)學 來源： 題型：解答題
某單位有員工1000名，平均每人每年創(chuàng)造利潤10萬元。為了增加企業(yè)競爭力，決定優(yōu)化產(chǎn)業(yè)結(jié)構(gòu)，調(diào)整出
名員工從事第三產(chǎn)業(yè)，調(diào)整后他們平均每人每年創(chuàng)造利為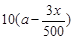
萬元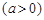
，剩下的員工平均每人每年創(chuàng)造的利潤可以提高
.
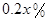（1）若要保證剩余員工創(chuàng)造的年總利潤不低于原來1000名員工創(chuàng)造的年總利潤，則最多調(diào)整出多少名員工從事第三產(chǎn)業(yè)？
（2）在（1）的條件下，若調(diào)整出的員工創(chuàng)造的年總利潤始終不高于剩余員工創(chuàng)造的年總利潤，則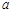
的取值范圍是多少？
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：解答題
已知函數(shù)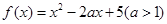
.
(1)若
的定義域和值域均是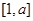
，求實數(shù)
的值；
(2)若在區(qū)間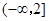
上是減函數(shù)，且對任意的
，
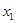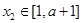，總有
，求實數(shù)的取值范圍.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：解答題
經(jīng)過長期觀測得到：在交通繁忙的時段內(nèi)，某公路段汽車的車流量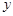
（千輛/時）與汽車的平均速度
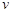（千米/時）之間的函數(shù)關(guān)系為
（
）．
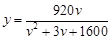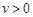（1）在該時段內(nèi)，當汽車的平均速度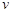為多少時，車流量最大？最大車流量為多少？
（2）若要求在該時段內(nèi)車流量超過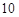
千輛/時，則汽車的平均速度應在什么范圍內(nèi)？
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：解答題
已知函數(shù)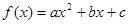
（a≠0）滿足
，
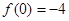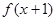為偶函數(shù)，且x＝－2是函數(shù)
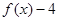的一個零點．又
（
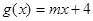＞0）．
（1）求函數(shù)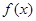
的解析式；
（2）若關(guān)于x 的方程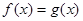
在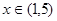
上有解，求實數(shù)的取值范圍；
（3）令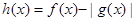
，求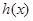
的單調(diào)區(qū)間．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：解答題
已知函數(shù)f(x)＝xm－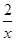
且f(4)＝
.
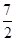(1)求m的值；
(2)判定f(x)的奇偶性；
(3)判斷f(x)在(0，＋∞)上的單調(diào)性，并給予證明．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：解答題
已知二次函數(shù)f(x)＝ax2＋bx＋c (a≠0)且滿足f(－1)＝0，對任意實數(shù)x，恒有f(x)－x≥0，并且當x∈(0,2)時，f(x)≤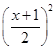
.
(1)求f(1)的值；
(2)證明：a>0，c>0；
(3)當x∈[－1,1]時，函數(shù)g(x)＝f(x)－mx (x∈R)是單調(diào)函數(shù)，求證：m≤0或m≥1.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
,
,
則
，
；由
可得
；對于（2）換元法是解題常用方法，可以減少許多不必要的運算量，提高解題效率，注意換元前后的對等關(guān)系，令
代入面積表達式可得：
.
為
,∴
，
,
取到最大值的情況，即為
, 即
是
上的奇函數(shù)，且當
時，
.
__________.