
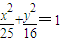 上的動點,F 是左焦點,當|AB|+
上的動點,F 是左焦點,當|AB|+ |BF|取最小值時,求B的坐標.
|BF|取最小值時,求B的坐標.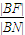 =
=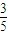 可求得BN|=
可求得BN|= |BF|,利用化折為直的思想即可求得當|AB|+
|BF|,利用化折為直的思想即可求得當|AB|+ |BF|取最小值時,B 的坐標.
|BF|取最小值時,B 的坐標.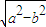 =
=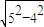 =3,
=3,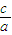 =
=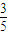 ,左準線為x=-
,左準線為x=-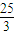 .
.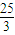 的垂線,垂足為N,過A作此準線的垂線,垂足為M.由橢圓定義,
的垂線,垂足為N,過A作此準線的垂線,垂足為M.由橢圓定義,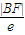 =
= |BF|.
|BF|. |BF|=|AB|+|BN|≥|AN|≥|AM|(定值),等號成立當且僅當B是AM與橢圓的交點時,此時B(-
|BF|=|AB|+|BN|≥|AN|≥|AM|(定值),等號成立當且僅當B是AM與橢圓的交點時,此時B(-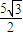 ,2)
,2) |BF|取最小值時,B的坐標為(
|BF|取最小值時,B的坐標為(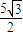 ,2).
,2). |BF|是關鍵,也是難點,屬于中檔題.
|BF|是關鍵,也是難點,屬于中檔題. 

 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:
| cosA |
| a |
| cosB |
| b |
| cosC |
| c |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com