
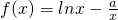 +1,其中a為實數:
+1,其中a為實數: ,求a的值.
,求a的值. +1,定義域為(0,+∞),x>0,
+1,定義域為(0,+∞),x>0,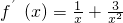
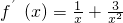 >0,
>0,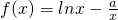 +1,
+1,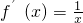 +
+ ,
,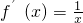 +
+ =0,得x=-a.
=0,得x=-a. ,a=-
,a=- <-1,不符題意,舍;
<-1,不符題意,舍; =
= ,a=-
,a=- >-e,不符題意,舍;
>-e,不符題意,舍; ,a=-e
,a=-e 滿足;
滿足; .
. +1,定義域為(0,+∞),x>0,知
+1,定義域為(0,+∞),x>0,知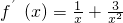 ,由此能夠證明f(x)在定義域(0,+∞)內為增函數.
,由此能夠證明f(x)在定義域(0,+∞)內為增函數.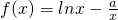 +1,知
+1,知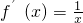 +
+ ,令f′(x)=0得x=-a,以-a在[1,e]內,左,右分為三類來討論,函數在[1,e]上的單調性,進而求出最值,令其等于32,求出a的值,由范圍來取舍,得出a的值.
,令f′(x)=0得x=-a,以-a在[1,e]內,左,右分為三類來討論,函數在[1,e]上的單調性,進而求出最值,令其等于32,求出a的值,由范圍來取舍,得出a的值.

 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:高中數學 來源: 題型:
(1)判斷函數y=logax的增減性;
(2)若命題p:|f(x)|<1-|f(2x)|為真命題,求實數x的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年浙江省溫州市高三八校聯考理科數學 題型:填空題
已知函數 ,
, ,其中a為常數,且函數y=f(x)和y=g(x)的圖像在其與兩坐標軸的交點處的切線相互平行.若關于x的不等式
,其中a為常數,且函數y=f(x)和y=g(x)的圖像在其與兩坐標軸的交點處的切線相互平行.若關于x的不等式 對任意不等于1的正實數都成立,則實數m的取值集合是____________。
對任意不等于1的正實數都成立,則實數m的取值集合是____________。
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江西省高三第一次月考試卷理科數學 題型:解答題
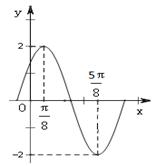
已知函數f(x)=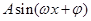 (其中A>0,
(其中A>0,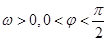 )的圖象如圖所示。
)的圖象如圖所示。
(1)求A,w及j的值;
(2)若tana=2,求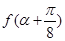 的值.
的值.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年福建省三明一中學高三(上)段考數學試卷(理科)(解析版) 題型:解答題
 +1,其中a為實數:
+1,其中a為實數: ,求a的值.
,求a的值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com