
某水產養殖場擬造一個無蓋的長方體水產養殖網箱,為了避免混養,箱中要安裝一些篩網,其平面圖如下,如果網箱四周網衣(圖中實線部分)建造單價為每米56元,篩網(圖中虛線部分)的建造單價為每米48元,網箱底面面積為160平方米,建造單價為每平方米50元,網衣及篩網的厚度忽略不計.
(1)把建造網箱的總造價y(元)表示為網箱的長x(米)的函數,并求出最低造價;
(2)若要求網箱的長不超過15米,寬不超過12米,則當網箱的長和寬各為多少米時,可使總造價最低?(結果精確到0.01米)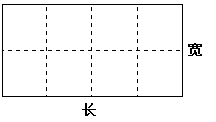
(1)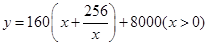 ,最低為13120元,(2)網箱長為15m,寬為10.67m時,可使總造價最低
,最低為13120元,(2)網箱長為15m,寬為10.67m時,可使總造價最低
解析試題分析:(1)建造網箱的總造價為網箱四周網衣建造總造價與篩網建造總造價之和. 網箱的長x,則 網箱的寬為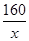 ,所以
,所以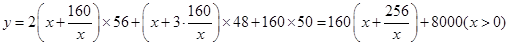 .當
.當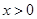 時,
時, ,當且僅當
,當且僅當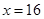 時取等號,此時
時取等號,此時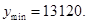 (2)因為網箱的長不超過15米,寬不超過12米,所以(1)中等號不成立.需從單調性上考慮最值. 因為
(2)因為網箱的長不超過15米,寬不超過12米,所以(1)中等號不成立.需從單調性上考慮最值. 因為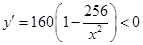 ,所以
,所以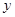 在
在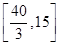 上單調遞減,而
上單調遞減,而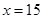 時,y最小,此時寬=
時,y最小,此時寬=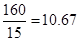 .
.
⑴網箱的寬為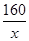 ,
,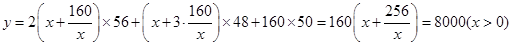 4分
4分
當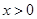 時,
時, ,當且僅當
,當且僅當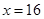 時取
時取
此時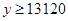
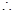 網箱的長為16m時,總造價最低為13120元 8分
網箱的長為16m時,總造價最低為13120元 8分
⑵由題意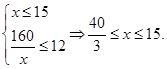 10分
10分
此時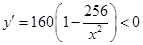 ,
,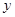 在
在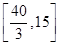 上單調遞減,而
上單調遞減,而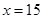 時,y最小,此時寬=
時,y最小,此時寬=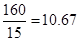 .
.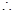 網箱長為15m,寬為10.67m時,可使總造價最低 16分
網箱長為15m,寬為10.67m時,可使總造價最低 16分
考點:函數應用題,利用不等式及導數求函數最值


科目:高中數學 來源: 題型:解答題
已知A、B、C是直線l上不同的三點,O是l外一點,向量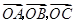 滿足:
滿足: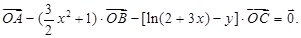 記y=f(x).
記y=f(x).
(1)求函數y=f(x)的解析式:
(2)若對任意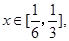 不等式
不等式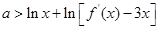 恒成立,求實數a的取值范圍:
恒成立,求實數a的取值范圍:
(3)若關于x的方程f(x)=2x+b在(0,1]上恰有兩個不同的實根,求實數b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數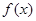 是定義在
是定義在 上的奇函數,當
上的奇函數,當 時,
時,  (其中e是自然界對數的底,
(其中e是自然界對數的底, )
)
(1)求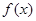 的解析式;
的解析式;
(2)設 ,求證:當
,求證:當 時,且
時,且 ,
,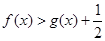 恒成立;
恒成立;
(3)是否存在實數a,使得當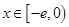 時,
時,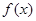 的最小值是3 ?如果存在,求出實數a的值;如果不存在,請說明理由。
的最小值是3 ?如果存在,求出實數a的值;如果不存在,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數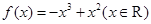 ,
, 滿足
滿足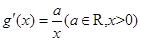 ,且
,且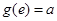 ,
, 為自然對數的底數.
為自然對數的底數.
(1)已知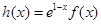 ,求
,求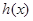 在
在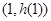 處的切線方程;
處的切線方程;
(2)若存在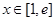 ,使得
,使得
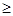
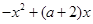 成立,求
成立,求 的取值范圍;
的取值范圍;
(3)設函數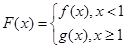 ,
, 為坐標原點,若對于
為坐標原點,若對于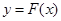 在
在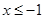 時的圖象上的任一點
時的圖象上的任一點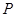 ,在曲線
,在曲線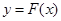
 上總存在一點
上總存在一點 ,使得
,使得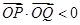 ,且
,且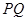 的中點在
的中點在 軸上,求
軸上,求 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com