
設(shè)函數(shù) 的定義域為
的定義域為
 ,值域為
,值域為 ,若
,若 的最小值為
的最小值為 ,則實(shí)數(shù)a的值為( )
,則實(shí)數(shù)a的值為( )
A. | B. 或 或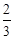 | C.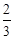 | D.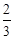 或 或 |
D
解析試題分析:①若1≤m<n,則f(x)=-logax,
∵f(x)的值域為[0,1],∴f(m)=0,f(n)=1,解得m=1,n=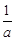 ,
,
又∵n-m的最小值為  ,∴
,∴ -1≥
-1≥ ,及0<a<1,當(dāng)?shù)忍柍闪r,解得a=
,及0<a<1,當(dāng)?shù)忍柍闪r,解得a= .
.
②若0<m<n<1,則f(x)=logax,
∵f(x)的值域為[0,1],∴f(m)=1,f(n)=0,解得m=a,n=1,又∵n-m的最小值為  ,∴1-a≥
,∴1-a≥ ,
,
及0<a<1,當(dāng)?shù)忍柍闪r,解得a=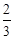 .
.
③若0<m<1<n時,不滿足題意,故選D。
考點(diǎn):本題主要考查對數(shù)函數(shù)的性質(zhì),絕對值的概念。
點(diǎn)評:中檔題,注意運(yùn)用分類討論思想,確定m,n,的可能情況。本題易錯,忽視不同情況的討論。



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:單選題
某公司生產(chǎn)甲、乙兩種桶裝產(chǎn)品,已知生產(chǎn)甲產(chǎn)品1桶需耗A原料l千克、B原料2千克;生產(chǎn)乙產(chǎn)品l桶需耗A原料2千克,B原料1千克.每桶甲產(chǎn)品的利潤是300元,每桶乙產(chǎn)品的利潤是400元.公司在生產(chǎn)這兩種產(chǎn)品的計劃中,要求每天消耗A、B原料都不超過12千克.通過合理安排生產(chǎn)計劃,從每天生產(chǎn)的甲、乙兩種產(chǎn)品中,公司共可獲得的最大利潤是
(A)2200元 (B)2400元
(C)2600元 (D)2800元
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com