
如圖,游客從某旅游景區的景點A處下山至C處有兩種路徑.一種是從A沿直線步行到C,另一種是先從A沿索道乘纜車到B,然后從B沿直線步行到C.現有甲、乙兩位游客從A處下山,甲沿AC勻速步行,速度為50 m/min.在甲出發2 min后,乙從A乘纜車到B,在B處停留1 min后,再從B勻速步行到C.假設纜車勻速直線運動的速度為130 m/min,山路AC長為1 260 m,經測量cos A= ,cos C=
,cos C= .
.

(1)求索道AB的長;
(2)問乙出發多少分鐘后,乙在纜車上與甲的距離最短?
(3)為使兩位游客在C處互相等待的時間不超過3分鐘,乙步行的速度應控制在什么范圍內?
(1)1040 m(2)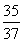 min(3)
min(3)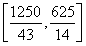
【解析】(1)在△ABC中,因為cos A=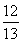 ,cos C=
,cos C=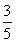 ,所以sin A=
,所以sin A=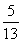 ,
,
sin C=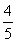 .
.
從而sin B=sin[π-(A+C)]=sin(A+C)=sin Acos C+cos Asin C=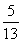 ×
×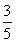 +
+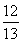 ×
×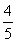 =
=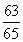 .
.

由正弦定理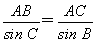 ,得AB=
,得AB=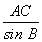 ×sin C=
×sin C= =1040(m).
=1040(m).
所以索道AB的長為1040 m.
(2)假設乙出發t分鐘后,甲、乙兩游客距離為d,此時,甲行走了(100+50t)m,乙距離A處130t m,所以由余弦定理得d2=(100+50t)2+(130t)2-2×130t×(100+50t)×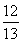 =200(37t2-70t+50),因0≤t≤
=200(37t2-70t+50),因0≤t≤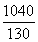 ,即0≤t≤8,故當t=
,即0≤t≤8,故當t=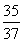 (min)時,甲、乙兩游客距離最短.
(min)時,甲、乙兩游客距離最短.
(3)由正弦定理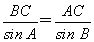 ,得BC=
,得BC=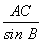 ×sin A=
×sin A=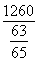 ×
×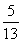 =500(m).
=500(m).
乙從B出發時,甲已走了50×(2+8+1)=550(m),還需走710 m才能到達C.
設乙步行的速度為v m/min,由題意得-3≤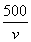 -
-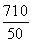 ≤3,解得
≤3,解得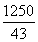 ≤v≤
≤v≤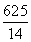 ,所以為使兩位游客在C處互相等待的時間不超過3分鐘,乙步行的速度應控制在
,所以為使兩位游客在C處互相等待的時間不超過3分鐘,乙步行的速度應控制在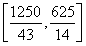 (單位:m/min)范圍內
(單位:m/min)范圍內


科目:高中數學 來源:2014年高考數學(文)二輪復習真題感悟江蘇專用常考問題1練習卷(解析版) 題型:填空題
已知f(x)是定義在R上的奇函數.當x>0時,f(x)=x2-4x,則不等式f(x)>x的解集用區間表示為________.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(文)二輪復習專題提升訓練江蘇專用階段檢測4練習卷(解析版) 題型:填空題
已知圓O的方程為x2+y2=2,圓M的方程為(x-1)2+(y-3)2=1,過圓M上任一點P作圓O的切線PA,若直線PA與圓M的另一個交點為Q,則當弦PQ的長度最大時,直線PA的斜率是________.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(文)二輪復習專題提升訓練江蘇專用階段檢測3練習卷(解析版) 題型:填空題
已知數列{an}是公差不為0的等差數列,{bn}是等比數列,其中a1=3,b1=1,a2=b2,3a5=b3,若存在常數u,v對任意正整數n都有an=3logubn+v,則u+v=________.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(文)二輪復習專題提升訓練江蘇專用階段檢測3練習卷(解析版) 題型:填空題
在等差數列{an}中,a8=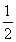 a11+6,則數列{an}前9項的和S9等于________.
a11+6,則數列{an}前9項的和S9等于________.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(文)二輪復習專題提升訓練江蘇專用階段檢測2練習卷(解析版) 題型:解答題
已知a=(sin α,1), b=(cos α,2),α∈ .
.
(1)若a∥b,求tan α的值;
(2)若a·b= ,求sin
,求sin  的值.
的值.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(文)二輪復習專題提升訓練江蘇專用階段檢測2練習卷(解析版) 題型:填空題
已知正△ABC的邊長為1,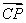 =7
=7  +3
+3 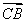 ,則
,則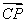 ·
·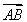 =________.
=________.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(文)二輪復習專題提升訓練江蘇專用階段檢測1練習卷(解析版) 題型:填空題
利民工廠某產品的年產量在100噸至300噸之間,年生產的總成本y(萬元)與年產量x(噸)之間的關系可近似地表示為y=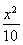 -30x+4 000,則每噸的成本最低時的年產量為________.
-30x+4 000,則每噸的成本最低時的年產量為________.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(文)二輪復習專題提升訓練江蘇專用7練習卷(解析版) 題型:填空題
已知α∈R,sin α+2cos α= ,則tan 2α等于________.
,則tan 2α等于________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com