
 平面ADC;
平面ADC;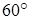
 出發的三條件直線兩兩垂直,從而
出發的三條件直線兩兩垂直,從而 ,又
,又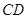 在平面
在平面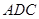 內,所以可證得平面ABC
內,所以可證得平面ABC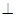 平面ADC.證明面面垂直向量法可證法向量垂直,由題意知從點
平面ADC.證明面面垂直向量法可證法向量垂直,由題意知從點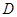 出發的三條件直線兩兩垂直,可以建立空間直角坐標系.
出發的三條件直線兩兩垂直,可以建立空間直角坐標系.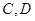 出發與棱
出發與棱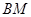 垂直的兩個向量所成的角.幾何法(三垂線法)重點是找到二面角的平面角,①在幾何體內找第三個平面與二面角的兩個半平都垂直,交線所成角即為平面角;如果找不到可以退而求其次,找第三個平面與二面角的其中一個半平垂直
垂直的兩個向量所成的角.幾何法(三垂線法)重點是找到二面角的平面角,①在幾何體內找第三個平面與二面角的兩個半平都垂直,交線所成角即為平面角;如果找不到可以退而求其次,找第三個平面與二面角的其中一個半平垂直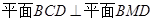 .②
.②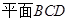 與另外一個半
與另外一個半 交于點
交于點 ,過點
,過點 作交線
作交線 的垂線
的垂線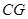 ③過點
③過點 作棱
作棱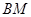 的垂線
的垂線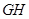 ④連
④連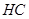 所得到的
所得到的 為二面角的平面角⑤在直角三角形
為二面角的平面角⑤在直角三角形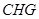 求角.用法向量法求二面角不容易判斷所求出的是二面角還是其補角,所以盡量不用它.
求角.用法向量法求二面角不容易判斷所求出的是二面角還是其補角,所以盡量不用它.
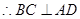

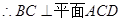 (4分)
(4分)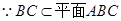
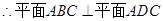 (6分)
(6分)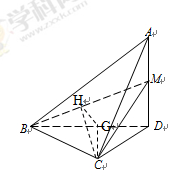

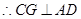
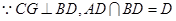
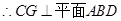
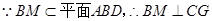
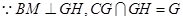
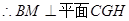

 =
=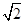 ,CG=CD
,CG=CD ,BG=BC
,BG=BC
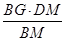 =
=
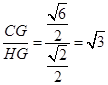
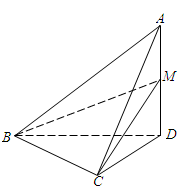
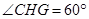 即二面角C-BM-D的大小為60°. (14分)
即二面角C-BM-D的大小為60°. (14分)

 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:高中數學 來源:不詳 題型:解答題
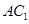 ∥平面
∥平面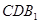 ;
;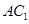 與
與 所成角的余弦值.
所成角的余弦值.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
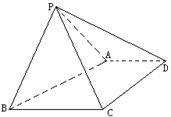
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 ,且AB=2AD=2DC=2PD=4,E為PA的中點.
,且AB=2AD=2DC=2PD=4,E為PA的中點.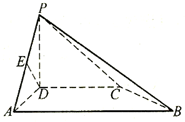
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 中,
中,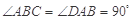 ,
,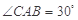 ,
,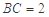 ,
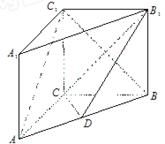
,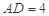 . 把
. 把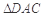 沿對角線
沿對角線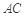 折起到
折起到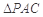 的位置,如圖2所示,使得點
的位置,如圖2所示,使得點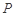 在平面
在平面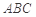 上的正投影
上的正投影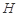 恰好落在線段
恰好落在線段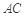 上,連接
上,連接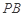 ,點
,點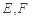 分別為線段
分別為線段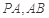 的中點.
的中點. 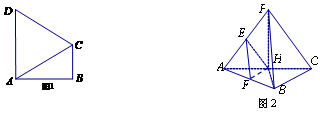
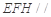 平面
平面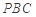 ;
;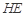 與平面
與平面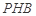 所成角的正弦值;
所成角的正弦值;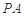 上是否存在一點
上是否存在一點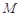 ,使得
,使得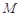 到點
到點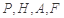 四點的距離相等?請說明理由.
四點的距離相等?請說明理由.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
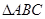 中,
中,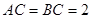 ,
,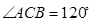 ,
,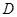 為
為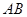 的中點,
的中點,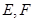 分別在線段
分別在線段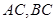 上的動點,且
上的動點,且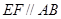 ,
,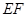 交
交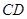 于
于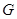 ,把
,把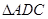 沿
沿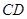 折起,如下圖所示,
折起,如下圖所示,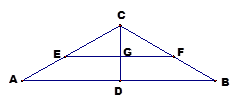
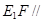 平面
平面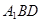 ;
;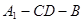 為直二面角時,是否存在點
為直二面角時,是否存在點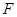 ,使得直線
,使得直線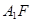 與平面
與平面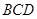 所成的角為
所成的角為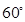 ,若存在求
,若存在求 的長,若不存在說明理由。
的長,若不存在說明理由。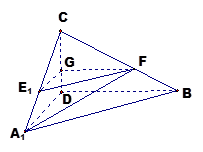
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com