
已知函數 ,
, .
.
(1)求函數 的最小正周期和單調增區間;
的最小正周期和單調增區間;
(2)求函數 在區間
在區間 上的最小值和最大值;
上的最小值和最大值;
(3)若 ,求使
,求使 的
的 取值范圍.
取值范圍.
(1)函數 的單調增區間是
的單調增區間是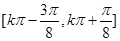 (
(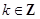 ),最小正周期為
),最小正周期為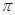 ;
;
(2) 在區間
在區間 上的最小值是
上的最小值是 ,最大值是
,最大值是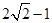 ;
;
(3)使 的
的 取值范圍是
取值范圍是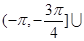
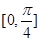
解析試題分析:(1)先對函數 利用三角恒等變換公式進行化簡,再利用周期公式求周期;根據化簡后的三角函數解析式,令
利用三角恒等變換公式進行化簡,再利用周期公式求周期;根據化簡后的三角函數解析式,令 ,
,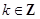 從中解出x的取值范圍,即可得到函數的單調遞減區間;
從中解出x的取值范圍,即可得到函數的單調遞減區間;
(3)由 得出的
得出的 取值范圍,然后再由正弦函數的性質求出
取值范圍,然后再由正弦函數的性質求出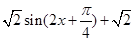 的
的 取值范圍,.
取值范圍,.
(3)由 得出的
得出的 取值范圍,然后再由正弦函數的性質求出
取值范圍,然后再由正弦函數的性質求出 中的取值范圍,兩者取交集即可得到
中的取值范圍,兩者取交集即可得到 取值范圍.
取值范圍.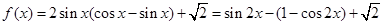
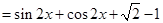
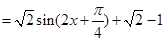
(1)函數 的最小正周期為
的最小正周期為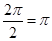 .
.
令 (
(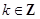 )得,
)得,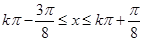 (
(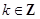 ).
).
所以函數 的單調增區間是
的單調增區間是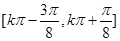 (
(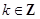 ).
).
(2)因為 ,所以
,所以 .
.
所以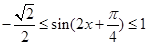 .
.
所以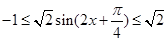 .
.
所以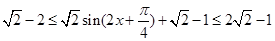 .
.
所以函數 在區間
在區間 上的最小值是
上的最小值是 ,最大值是
,最大值是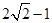 .
.
(3) 因為 ,所以
,所以 .
.
由 得,
得, ,
,
所以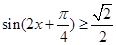 .
.
所以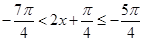 或
或 .
.
所以 或
或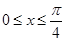 .
.
當 時,使
時,使 的
的 取值范圍是
取值范圍是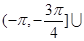
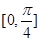 .
.
考點:正弦函數的性質及其應用


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案科目:高中數學 來源: 題型:解答題
某同學用“五點法”畫函數 在某一個周期內的圖象時,列表并填入的部分數據如下表:
在某一個周期內的圖象時,列表并填入的部分數據如下表:
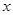 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
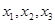 ,并直接寫出函數
,并直接寫出函數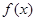 的解析式;
的解析式;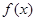 的圖象沿
的圖象沿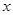 軸向右平移
軸向右平移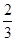 個單位得到函數
個單位得到函數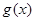 ,若函數
,若函數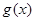 在
在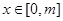 (其中
(其中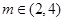 )上的值域為
)上的值域為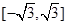 ,且此時其圖象的最高點和最低點分別為
,且此時其圖象的最高點和最低點分別為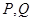 ,求
,求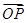 與
與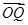 夾角
夾角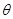 的大小。
的大小。查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=2cosxsin(x+ )-
)- sin2x+sinxcosx.
sin2x+sinxcosx.
(1)求函數f(x)的單調遞減區間;
(2)將函數f(x)的圖象沿x軸向右平移m個單位后的圖象關于直線x= 對稱,求m的最小正值.
對稱,求m的最小正值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,某污水處理廠要在一正方形污水處理池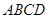 內修建一個三角形隔離區以投放凈化物質,其形狀為三角形
內修建一個三角形隔離區以投放凈化物質,其形狀為三角形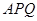 ,其中
,其中 位于邊
位于邊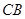 上,
上,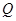 位于邊
位于邊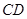 上.已知
上.已知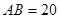 米,
米,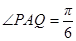 ,設
,設 ,記
,記 ,當
,當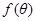 越大,則污水凈化效果越好.
越大,則污水凈化效果越好.
(1)求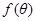 關于的函數解析式,并求定義域;
關于的函數解析式,并求定義域;
(2)求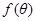 最大值,并指出等號成立條件?
最大值,并指出等號成立條件?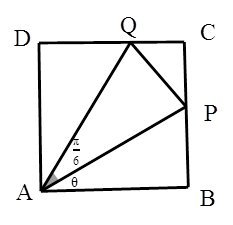
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com