（12分）某企業擬在2012年度進行一系列促銷活動，已知某產品年銷量x萬件與年促銷費用t萬元之間滿足3-x與t+1成反比例，當年促銷費用t=0萬元時，年銷量是1萬件，已知2012年產品的設備折舊、維修等固定費用為3萬元，每生產1萬件產品需再投入32萬元的生產費用。若將每件產品售價定為：其生產成本的150%與“平均每件促銷費的一半”之和，則當年生產的商
（1）將2012年的利潤y（萬元）表示為促銷費t（萬元）的函數
（2）該企業2012年的促銷費投入多少萬元時，企業年利潤最大？（注：利潤=銷售收入-生產成
本-促銷費，生產成本=固定費用+生產費用）
科目：高中數學 來源： 題型：解答題
（本小題滿分12分）
已知二次函數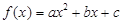
.
（1）若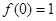
，
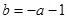，解關于x不等式
;
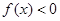（2）若f(x)的最小值為0，且A.<b，設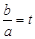
，請把
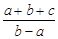表示成關于t的函數g(t)，并求g(t)的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（本小題滿分14分）某城市自西向東和自南向北的兩條主干道的東南方位有一塊空地市規劃部門計劃利用它建設一個供市民休閑健身的小型綠化廣場，如下圖所示是步行小道設計方案示意圖，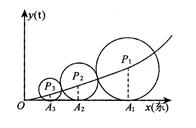
其中，
分別表示自西向東，自南向北的兩條主干道.設計方案是自主干道交匯點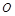
處修一條步行小道，小道為拋物線
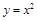的一段，在小道上依次以點
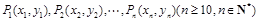為圓心，修一系列圓型小道，這些圓型小道與主干道
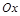相切，且任意相鄰的兩圓彼此外切，若
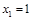（單位：百米）且
.
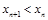（1）記以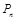
為圓心的圓與主干道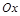切于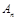
點，證明：數列
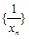是等差數列，并求
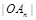關于
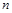的表達式；
（2）記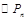
的面積為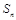
，根據以往施工經驗可知，面積為
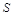的圓型小道的施工工時為
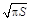（單位：周）.試問5周時間內能否完成前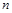個圓型小道的修建？請說明你的理由.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知二次函數f(x)=ax2+bx,f(x+1)為偶函數,函數f(x)的圖象與直線y=x相切.
（I）求f(x)的解析式;
（II）已知k的取值范圍為[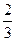
,+∞),則是否存在區間[m,n](m<n),使得f(x)在區間[m,n]上的值域恰好為[km,kn]?若存在,請求出區間[m,n];若不存在,請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某地區預計明年從年初開始的前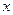
個月內，對某種商品的需求總量
（萬件）與月份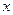的近似關系為
.
（1）寫出明年第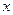個月的需求量
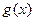（萬件）與月份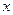的函數關系式，并求出哪個月份的需求量超過1.4萬件；
（2）如果將該商品每月都投放市場p萬件，要保持每月都滿足市場需求，則p至少為多少萬件
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
；（2）t=7 
.
+
的值,
,且
求
.
的的定義域為
.當
時，求函數
的最值及相應的
的值。
函數
是增函數，
函數
在R上有極值，求使命題“p且q”為真的實數m的取值范圍。
（1）解不等式
； （2）求函數
的值域.