
 殘骸,我國“雪龍號”科考船于2014年3月26日從港口
殘骸,我國“雪龍號”科考船于2014年3月26日從港口 出發,沿北偏東
出發,沿北偏東 角的射線
角的射線 方向航行,而在港口北偏東
方向航行,而在港口北偏東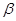 角的方向上有一個給科考船補給物資的小島
角的方向上有一個給科考船補給物資的小島 ,
, 海里,且
海里,且
 .現指揮部需要緊急征調位于港口
.現指揮部需要緊急征調位于港口 正東
正東 海里的
海里的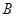 處的補給船,速往小島
處的補給船,速往小島 裝上補給物資供給科考船.該船沿
裝上補給物資供給科考船.該船沿 方向全速追趕科考船,并在
方向全速追趕科考船,并在 處相遇.經測算當兩船運行的航線與海岸線
處相遇.經測算當兩船運行的航線與海岸線 圍成的三角形
圍成的三角形 的面積
的面積 最小時,這種補給方案最優.
最小時,這種補給方案最優.
 關于
關于 的函數關系式
的函數關系式 ;
;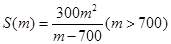 ;(2)1400.
;(2)1400.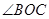 是固定的,點
是固定的,點 也是不變,直線
也是不變,直線 過點
過點 ,要求
,要求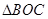 面積的最小值,根據已知條件,我們用解析法來解題,以
面積的最小值,根據已知條件,我們用解析法來解題,以 為坐標原點,向東方向為
為坐標原點,向東方向為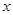 正半軸,向北方向為
正半軸,向北方向為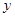 軸正半軸,建立直角坐標系,則可得直線
軸正半軸,建立直角坐標系,則可得直線 的方程為
的方程為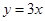 ,點
,點 坐標為
坐標為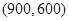 ,又有點
,又有點 坐標為
坐標為 ,可得直線
,可得直線 方程,它與直線
方程,它與直線 的交點
的交點 的坐標可解得,而
的坐標可解得,而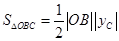 ,這樣要求的表達式就可得;(2)在(1)基礎上,
,這樣要求的表達式就可得;(2)在(1)基礎上,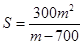 ,其最小值求法,把分式的分子分母同時除以
,其最小值求法,把分式的分子分母同時除以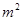 ,得
,得 ,分母是關于
,分母是關于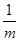 的二次函數,最值易求.
的二次函數,最值易求.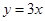 ,設點A(x0,y0),則
,設點A(x0,y0),則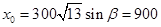 ,
,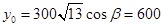 ,即A(900,600), (3分)
,即A(900,600), (3分)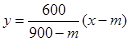 , (4分)
, (4分)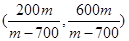 , (6分)
, (6分)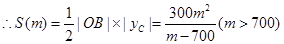 (8分)
(8分)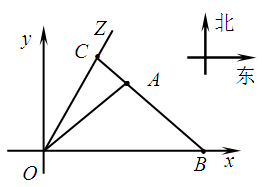
 (10分)
(10分)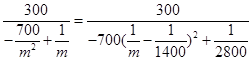 (12分)
(12分)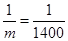 ,即
,即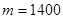 時,
時, 最小,
最小,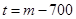 ,則
,則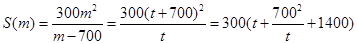
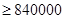 ,當且僅當
,當且僅當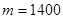 時,
時, 最小)
最小)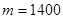 海里處的船只時,補給方案最優. (14分)
海里處的船只時,補給方案最優. (14分)

 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:不詳 題型:解答題
 為圓心的兩個同心圓弧
為圓心的兩個同心圓弧 、弧
、弧 以及兩條線段
以及兩條線段 和
和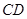 圍成的封閉圖形.花壇設計周長為30米,其中大圓弧
圍成的封閉圖形.花壇設計周長為30米,其中大圓弧 所在圓的半徑為10米.設小圓弧
所在圓的半徑為10米.設小圓弧 所在圓的半徑為
所在圓的半徑為 米(
米( ),圓心角為
),圓心角為 弧度.
弧度.
 關于
關于 的函數關系式;
的函數關系式; ,當
,當 為何值時,
為何值時, 取得最大值?
取得最大值?查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
 (x)=-x(x+1),則函數g(x)=f(logax)(0<a<1)的單調遞減區間是( )
(x)=-x(x+1),則函數g(x)=f(logax)(0<a<1)的單調遞減區間是( )| A.[-1,0] | B.[ ,+∞),(0,1] ,+∞),(0,1] |
C.[1,  ] ] | D.(-∞, ) ,( ) ,( ,+∞) ,+∞) |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
 的隧道時,整個車身都在隧道里的時間是
的隧道時,整個車身都在隧道里的時間是 .該列車以同樣的速度穿過長790
.該列車以同樣的速度穿過長790 的鐵橋時,從車頭上橋,到車尾下橋,共用時
的鐵橋時,從車頭上橋,到車尾下橋,共用時 ,則這列火車的長度為___
,則這列火車的長度為___ .
.查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| A.y=x2 | B.y=x+1 | C.y=2x | D.y=log2|x| |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com