
已函數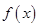 是定義在
是定義在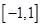 上的奇函數,在
上的奇函數,在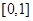 上
上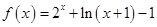 .
.
(1)求函數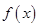 的解析式;并判斷
的解析式;并判斷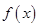 在
在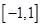 上的單調性(不要求證明);
上的單調性(不要求證明);
(2)解不等式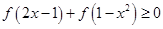 .
.
(1)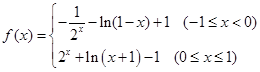 ,
, 是
是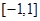 上增函數;(2)不等式的解集為
上增函數;(2)不等式的解集為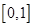 .
.
解析試題分析:(1)這是由函數的對稱性求函數的解析式問題,先設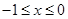 ,進而得到
,進而得到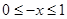 ,根據奇函數的定義即可得出
,根據奇函數的定義即可得出

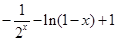 ,從而可寫出函數的解析式,對于函數的單調性則根據指數函數、對數函數的單調性及奇函數的性質進行判斷即可;(2)先根據奇函數的定義進行化簡不等式,轉化為
,從而可寫出函數的解析式,對于函數的單調性則根據指數函數、對數函數的單調性及奇函數的性質進行判斷即可;(2)先根據奇函數的定義進行化簡不等式,轉化為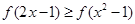 ,進而根據函數的單調性與定義域,列出不等式組
,進而根據函數的單調性與定義域,列出不等式組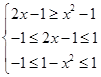 ,從中求解該不等式組即可.
,從中求解該不等式組即可.
試題解析:(1)設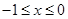 ,則
,則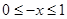
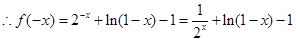
又 是奇函數,所以
是奇函數,所以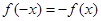 ,
,

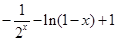 3分
3分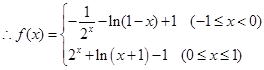
當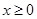 時,
時,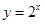 、
、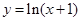 單調遞增,所以
單調遞增,所以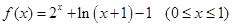 單調遞增且
單調遞增且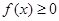 ,由奇函數的性質可知
,由奇函數的性質可知 在
在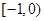 也單調遞增且
也單調遞增且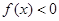
所以 是
是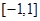 上的增函數
上的增函數
(2)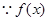 是
是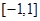 上增函數,由已知得
上增函數,由已知得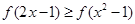
等價于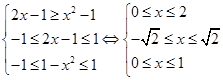
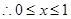
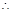 不等式的解集為
不等式的解集為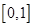 .
.
考點:1.函數的奇偶性;2.分段函數的解析式求法;3.基本初等函數的圖像與性質;4.函數的單調性及其應用.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
已知函數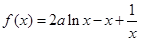 (
( 且
且 ),
),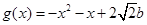
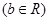 .
.
(1)若 在定義域上有極值,求實數
在定義域上有極值,求實數 的取值范圍;
的取值范圍;
(2)當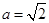 時,若對
時,若對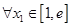 ,總
,總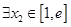 ,使得
,使得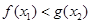 ,求實數
,求實數 的取值范圍;(其中
的取值范圍;(其中 為自然對數的底數)
為自然對數的底數)
(3)對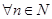 ,且
,且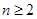 ,證明:
,證明: 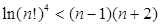 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在扶貧活動中,為了盡快脫貧(無債務)致富,企業甲將經營狀況良好的某種消費品專賣店以5.8萬元的優惠價格轉讓給了尚有5萬元無息貸款沒有償還的小型企業乙,并約定從該店經營的利潤中,首先保證企業乙的全體職工每月最低生活費的開支3 600無后,逐步償還轉讓費(不計息).在甲提供的資料中有:①這種消費品的進價為每件14元;②該店月銷量Q(百件)與銷售價格P(元)的關系如圖所示;③每月需要各種開支2 000元.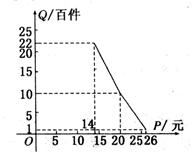
(1)當商品的價格為每件多少元時,月利潤扣除職工最低生活費的余額最大?并求最大余額;
(2)企業乙只依靠該店,最早可望在幾年后脫貧?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
對于定義域為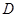 的函數
的函數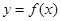 ,若同時滿足:
,若同時滿足:
① 在
在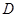 內單調遞增或單調遞減;
內單調遞增或單調遞減;
②存在區間[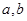 ]
]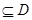 ,使
,使 在
在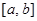 上的值域為
上的值域為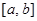 ;
;
那么把函數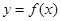 (
(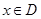 )叫做閉函數.
)叫做閉函數.
(1) 求閉函數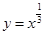 符合條件②的區間
符合條件②的區間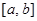 ;
;
(2) 若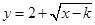 是閉函數,求實數
是閉函數,求實數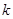 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知定義域為 的函數
的函數 同時滿足以下三個條件:
同時滿足以下三個條件:
(1) 對任意的 ,總有
,總有 ;(2)
;(2) ;(3) 若
;(3) 若 ,
, ,且
,且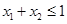 ,則有
,則有 成立,則稱
成立,則稱 為“友誼函數”,請解答下列各題:
為“友誼函數”,請解答下列各題:
(1)若已知 為“友誼函數”,求
為“友誼函數”,求 的值;
的值;
(2)函數 在區間
在區間 上是否為“友誼函數”?并給出理由.
上是否為“友誼函數”?并給出理由.
(3)已知 為“友誼函數”,假定存在
為“友誼函數”,假定存在 ,使得
,使得 且
且 , 求證:
, 求證: .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com