Question

設x，y滿足條件

x+y≤3 y≤x-1 y≥0

，則w=e(x+1)2+y2的最小值

 

．

Answer 1

分析：本題屬于線性規劃中的延伸題，先將求w的最小值問題轉化成求指數式：（x+1）²+y²的最小值．對于可行域不要求線性目標函數的最值，而是求可行域內的點與原點（-1，0）構成的線段的長度問題．

解答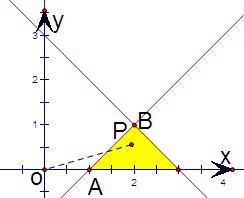：解：先根據約束條件畫出可行域，
z=（x+1）²+y²，
表示可行域內點到點（-1，0）距離OP的平方，
當P在點A時，z最小，最小值為2²+0²=4，
則w=e(x+1)2+y2的最小值為：e⁴
故答案為：e⁴．

點評：本題主要考查了用平面區域二元一次不等式組，以及簡單的轉化思想和數形結合的思想，屬中檔題．巧妙識別目標函數的幾何意義是我們研究規劃問題的基礎，縱觀目標函數包括線性的與非線性，非線性問題的介入是線性規劃問題的拓展與延伸，使得規劃問題得以深化．