
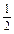 x,求使f(x)=-
x,求使f(x)=-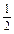 在[0,2 009]上的所有x的個數.
在[0,2 009]上的所有x的個數.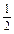
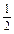 x,
x,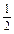 (-x)=-
(-x)=-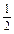 x.
x.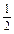 x,即f(x)=
x,即f(x)=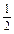 x. 7分
x. 7分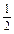 x(-1≤x≤1) 8分
x(-1≤x≤1) 8分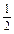 (x-2), 10分
(x-2), 10分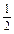 (x-2),
(x-2),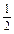 (x-2)(1<x<3). 11分
(x-2)(1<x<3). 11分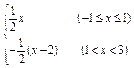 12分
12分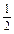 ,解得x=-1.
,解得x=-1.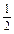 的所有x="4n-1" (n∈Z). 14分
的所有x="4n-1" (n∈Z). 14分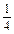 ≤n≤
≤n≤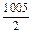 ,
,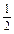 . 16分
. 16分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源:不詳 題型:解答題
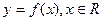 滿足
滿足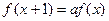 ,
,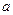 是不為
是不為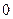 的實常數。
的實常數。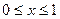 時,
時,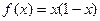 ,求函數
,求函數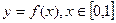 的值域;
的值域;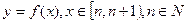 的解析式;
的解析式;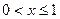 時,
時,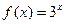 ,試研究函數
,試研究函數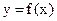 在區間
在區間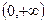 上是否可能是單調函數?
上是否可能是單調函數?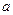 的取值范圍;若不可能,請說明理由。
的取值范圍;若不可能,請說明理由。查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
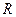 上的函數
上的函數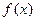 不是常數函數,且滿足對任意的
不是常數函數,且滿足對任意的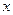 ,
,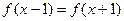 ,
,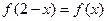 ,現得出下列5個結論:①
,現得出下列5個結論:①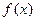 是偶函數,②
是偶函數,②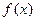 的圖像關于
的圖像關于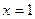 對稱,③
對稱,③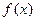 是周期函數,④
是周期函數,④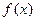 是單調函數,⑤
是單調函數,⑤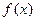 有最大值和最小值。其中正確的命題是 ( )
有最大值和最小值。其中正確的命題是 ( )查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
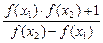 ;
; 求證:
求證: 查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com