
已知函數 ,其中
,其中 且
且 .
.
(1)求證:函數 在點
在點 處的切線與
處的切線與 總有兩個不同的公共點;
總有兩個不同的公共點;
(2)若函數 在區間
在區間 上有且僅有一個極值點,求實數
上有且僅有一個極值點,求實數 的取值范圍.
的取值范圍.
(1)詳見解析;(2)實數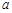 的取值范圍是
的取值范圍是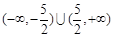 .
.
解析試題分析:(1)求證:函數 在點
在點 處的切線與
處的切線與 總有兩個不同的公共點,先求出函數
總有兩個不同的公共點,先求出函數 在點
在點 處的切線方程,因此對函數
處的切線方程,因此對函數 求導得
求導得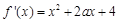 ,從而得
,從而得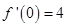 ,再求出
,再求出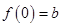 ,由點斜式即可得切線方程
,由點斜式即可得切線方程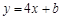 ,證切線與
,證切線與 總有兩個不同的公共點,即方程
總有兩個不同的公共點,即方程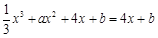 有兩個不同的解,即
有兩個不同的解,即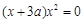 有兩個不同的解,由已知
有兩個不同的解,由已知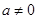 ,故方程存在兩解,既得證.(2)若函數
,故方程存在兩解,既得證.(2)若函數 在區間
在區間 上有且僅有一個極值點,只需
上有且僅有一個極值點,只需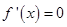 在區間
在區間 上有且僅有一個解,且在解的兩邊異號,而
上有且僅有一個解,且在解的兩邊異號,而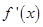 是二次函數,故只需
是二次函數,故只需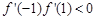 ,即可求出
,即可求出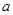 的取值范圍.
的取值范圍.
(1)由已知可得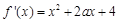 . 1分
. 1分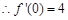 , 2分
, 2分
又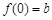 ,
,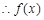 在
在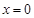 處的切線方程為
處的切線方程為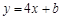 . 4分
. 4分
令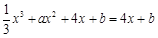 ,整理得
,整理得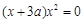 .
.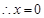 或
或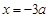 , 5分
, 5分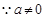
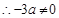 , 6分
, 6分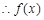 與切線有兩個不同的公共點. 7分
與切線有兩個不同的公共點. 7分
(2)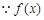 在
在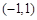 上有且僅有一個極值點,
上有且僅有一個極值點,
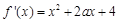 在
在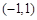 上有且僅有一個異號零點, 9分
上有且僅有一個異號零點, 9分
由二次函數圖象性質可得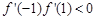 , 10分
, 10分
即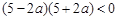 ,解得
,解得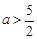 或
或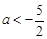 , 12分
, 12分
綜上,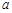 的取值范圍是
的取值范圍是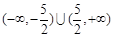 . 13分
. 13分
考點:導數的幾何意義,函數的極值.


科目:高中數學 來源: 題型:解答題
若函數y=f(x)在x=x0處取得極大值或極小值,則稱x0為函數y=f(x)的極值點.已知a,b是實數,1和-1是函數f(x)=x3+ax2+bx的兩個極值點.
(1)求a和b的值;
(2)設函數g(x)的導函數g′(x)=f(x)+2,求g(x)的極值點.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=x2+ax+b,g(x)=ex(cx+d).若曲線y=f(x)和曲線y=g(x)都過點P(0,2),且在點P處有相同的切線y=4x+2.
(1)求a,b,c,d的值;
(2)若x≥-2時,f(x)≤kg(x),求k的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com