
已知數列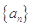 的首項
的首項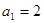 ,且對任意
,且對任意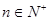 都有
都有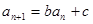 (其中
(其中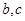 為常數).
為常數).
(1)若數列 為等差數列,且
為等差數列,且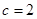 ,求
,求 的通項公式.
的通項公式.
(2)若數列 是等比數列,且
是等比數列,且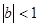 ,從數列
,從數列 中任意取出相鄰的三項,均能按某種順序排成等差數列,求
中任意取出相鄰的三項,均能按某種順序排成等差數列,求 的前
的前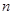 項和
項和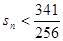 成立的
成立的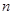 的取值的集合.
的取值的集合.
(1)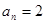 或
或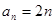 ;(2){2,4,6,8} .
;(2){2,4,6,8} .
解析試題分析:(1)對實數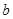 分類討論,①
分類討論,①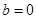 ,
,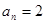 ;②
;②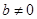 時,根據等差數列的定義,可知
時,根據等差數列的定義,可知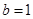 ,公差
,公差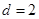 ,則
,則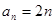 ;(2)若數列
;(2)若數列 為等比數列,則
為等比數列,則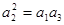 ,即
,即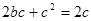 ,因此
,因此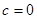 (注意
(注意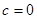 是容易漏掉的)或
是容易漏掉的)或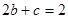 , 在這
, 在這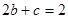 情況下,可得
情況下,可得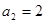 ,故
,故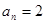 不滿足
不滿足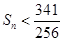 ,因此只有
,因此只有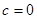 滿足條件,由任相鄰的三項均能按某種順序排成等差數列,可分為以下三種情況:①
滿足條件,由任相鄰的三項均能按某種順序排成等差數列,可分為以下三種情況:①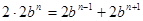 ;②
;②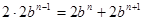 ;③
;③ ,分別求出
,分別求出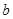 看是否滿足條件,由滿足條件的
看是否滿足條件,由滿足條件的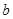 結合
結合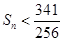 確定
確定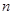 的取值的個數.
的取值的個數.
(1)當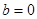 時,
時,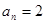 符合題意,
符合題意,
當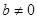 時,由于數列
時,由于數列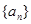 是等差數列且
是等差數列且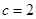 ,所以
,所以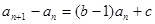 為常數,故
為常數,故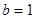 ,得
,得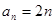 ,
,
所以,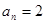 或
或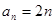 .(6分)(只求得一個得3分)
.(6分)(只求得一個得3分)
(2)由數列 為等比數列,所以
為等比數列,所以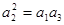 得
得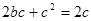
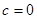 或
或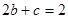 , (8分)
, (8分)
若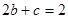 得
得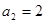 ,故
,故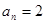 不滿足
不滿足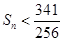
所以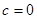 ,得
,得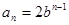 .
.
由任相鄰的三項均能按某種順序排成等差數列,即
若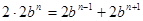 得
得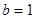 (舍).
(舍).
若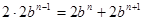 得
得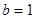 (舍)或
(舍)或 (舍),
(舍),
若 得
得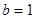 舍或
舍或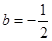 ,
,
故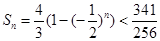 得
得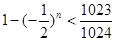
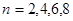 即所求值的集合為{2,4,6,8} (13分)
即所求值的集合為{2,4,6,8} (13分)
考點:等差數列、等比數列的性質.


 智能訓練練測考系列答案
智能訓練練測考系列答案 計算高手系列答案
計算高手系列答案科目:高中數學 來源: 題型:解答題
設等比數列{an}的前n項和為Sn,已知an + 1 = 2Sn + 2 (n∈N*).
(1)求數列{an}的通項公式;
(2)在an與an + 1之間插入n個數,使這n + 2個數組成一個公差為dn的等差數列.
①在數列{dn}中是否存在三項dm,dk,dp (其中m,k,p成等差數列)成等比數列?若存在,求出這樣的三項,若不存在,說明理由;
②求證: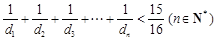 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知等差數列{an}前三項的和為-3,前三項的積為8.
(1) 求等差數列{an}的通項公式;
(2) 若數列{an}單調遞增,求數列{an}的前n項和.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知數列{an}是公差不為0的等差數列,a1=2,且a2,a3,a4+1成等比數列.
(1)求數列{an}的通項公式;
(2)設bn=an+2an,求數列{bn}的前n項和Sn.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如果數列 滿足:
滿足: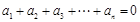 且
且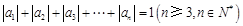 ,則稱數列
,則稱數列 為
為 階“歸化數列”.
階“歸化數列”.
(1)若某4階“歸化數列” 是等比數列,寫出該數列的各項;
是等比數列,寫出該數列的各項;
(2)若某11階“歸化數列” 是等差數列,求該數列的通項公式;
是等差數列,求該數列的通項公式;
(3)若 為n階“歸化數列”,求證:
為n階“歸化數列”,求證: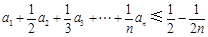 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知數列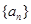 的各項均為正數,記
的各項均為正數,記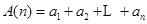 ,
,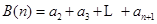 ,
,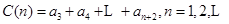 .
.
(1)若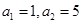 ,且對任意
,且對任意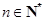 ,三個數
,三個數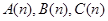 組成等差數列,求數列
組成等差數列,求數列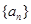 的通項公式.
的通項公式.
(2)證明:數列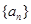 是公比為
是公比為 的等比數列的充分必要條件是:對任意
的等比數列的充分必要條件是:對任意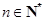 ,三個數
,三個數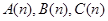 組成公比為
組成公比為 的等比數列.
的等比數列.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com