
(本小題滿分12分)已知x∈[- ,
, ],f(x)=tan2x+2tan x+2,求f(x)的最大值和最小值,并求出相應的x值.
],f(x)=tan2x+2tan x+2,求f(x)的最大值和最小值,并求出相應的x值.
當tan x=-1,即x=- 時, y有最小值,ymin=1;當tan x=1,即x=
時, y有最小值,ymin=1;當tan x=1,即x= 時,y有最大值,ymax=5.
時,y有最大值,ymax=5.
解析試題分析:解f(x)=tan2x+2tan x+2=(tan x+1)2+1. ……………2
∵x∈[- ,
, ],∴tan x∈[-
],∴tan x∈[-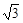 ,1]. ……………6
,1]. ……………6
∴當tan x=-1,即x=- 時, y有最小值,ymin=1;……………9
時, y有最小值,ymin=1;……………9
當tan x=1,即x= 時,y有最大值,ymax=5. ……………12
時,y有最大值,ymax=5. ……………12
考點:二次函數在某閉區間上的最值問題;正切函數的值域。
點評:影響二次函數在閉區間上的最值主要有三個因素:拋物線的開口方向、對稱軸和區間的位置。我們常見的并且感到困難的主要是這兩類問題:一是動軸定區間,二是定軸動區間。此題是最簡單、最基礎的二次函數在閉區間上的求最值問題。


 課課練江蘇系列答案
課課練江蘇系列答案 名牌中學課時作業系列答案
名牌中學課時作業系列答案科目:高中數學 來源: 題型:解答題
(本題滿分13分)已知函數f(x)=cos(- )+cos(
)+cos( ),k∈Z,x∈R.
),k∈Z,x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)在[0,π)上的減區間;
(3)若f(α)= ,α∈(0,
,α∈(0, ),求tan(2α+
),求tan(2α+ )的值.
)的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分13分)函數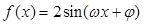
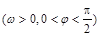 的部分圖象如下圖所示,該圖象與
的部分圖象如下圖所示,該圖象與 軸交于點
軸交于點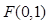 ,與
,與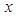 軸交于點
軸交于點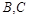 ,
, 為最高點,且
為最高點,且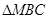 的面積為
的面積為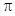 .
.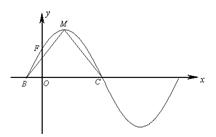
(Ⅰ)求函數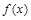 的解析式;
的解析式;
(Ⅱ)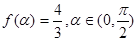 ,求
,求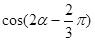 的值.
的值.
(Ⅲ)將函數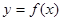 的圖象的所有點的橫坐標縮短到原來的
的圖象的所有點的橫坐標縮短到原來的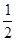 倍(縱坐標不變),再向左平移
倍(縱坐標不變),再向左平移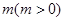 個單位,得函數
個單位,得函數 的圖象,若函數
的圖象,若函數 為奇函數,求
為奇函數,求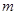 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com