
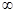 ),都有f(x)<0,求a的取值范圍.
),都有f(x)<0,求a的取值范圍.科目:高中數學 來源:不詳 題型:解答題
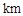 ,貨車從甲地勻速行駛到乙地,速度不得超過80
,貨車從甲地勻速行駛到乙地,速度不得超過80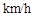 ,已知貨車每小時的運輸成本(單位:元)由可變成本和固定成本組成,可變成本是速度平方的
,已知貨車每小時的運輸成本(單位:元)由可變成本和固定成本組成,可變成本是速度平方的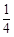 倍,固定成本為a元.
倍,固定成本為a元.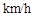 )的函數,并指出這個函數的定義域;
)的函數,并指出這個函數的定義域;查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
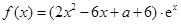 (
(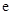 為自然對數的底數).
為自然對數的底數).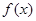 在
在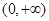 上的單調區間;
上的單調區間;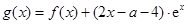 ,是否存在區間
,是否存在區間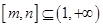 ,使得當
,使得當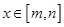 時函數
時函數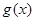 的值域為
的值域為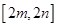 ,若存在求出
,若存在求出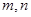 ,若不存在說明理由.
,若不存在說明理由.查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
 f’(x)<0,又a=f(log0.53),b=f((
f’(x)<0,又a=f(log0.53),b=f((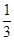 )0.3),c=f(ln3),則( )
)0.3),c=f(ln3),則( )| A.a<b<c | B.b<c<a | C.c<a<b | D.c< b<a |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com