
(09年泗陽中學模擬六)(14分) 如圖,在多面體ABCDE中,AE⊥ABC,BD∥AE,
且AC=AB=BC=BD=2,AE=1,F在CD上(不含C, D兩點)
(1)求多面體ABCDE的體積;
(2)若F為CD中點,求證:EF⊥面BCD;
(3)當![]() 的值= 時,能使AC ∥平面EFB,并給出證明。
的值= 時,能使AC ∥平面EFB,并給出證明。

解析:(1)設AB中點為H,則由AC=AB=BC=2,可得CH⊥AB且CH=.
又BD∥AE,所以BD與AE共面.
又AE⊥面ABC,所以平面ABDE⊥平面ABC.
所以CH⊥平面ABDE,即CH為四棱錐C-ABDE的高.
故四棱錐C-ABDE的體積為VC-ABDE=SABDE?CH=[(1+2)×2×]=.
(2)取BC中點G,連FG,AG.
因為AE⊥面ABC,BD∥AE,所以BD⊥面ABC.
又AGÌ面ABC,所以BD⊥AG.
又AC=AB,G是BC的中點,所以AG⊥BC,所以AG![]() 平面BCD.
平面BCD.
又因為F是CD的中點且BD=2,所以FG∥BD且FG=BD=1,所以FG∥AE.
又AE=1,所以AE=FG,所以四邊形AEFG是平行四邊形,
所以EF∥AG,所以EF⊥BCD.
(3)![]() =2(證明過程略)。
=2(證明過程略)。


科目:高中數學 來源: 題型:
(09年泗陽中學模擬六)(15分)已知m∈R,直線l:![]() 和圓C:
和圓C:![]() 。
。
(1)求直線l斜率的取值范圍;
(2)直線l能否將圓C分割成弧長的比值為![]() 的兩段圓弧?為什么?
的兩段圓弧?為什么?
查看答案和解析>>
科目:高中數學 來源: 題型:
(09年泗陽中學模擬六)(15分
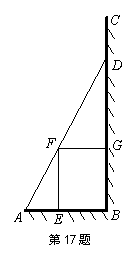
如圖,某小區準備在一直角圍墻![]() 內的空地上植造一塊“綠地
內的空地上植造一塊“綠地![]() ”,其中
”,其中![]() 長為定值
長為定值![]() ,
,![]() 長可根據需要進行調節(
長可根據需要進行調節(![]() 足夠長).現規劃在
足夠長).現規劃在![]() 的內接正方形
的內接正方形![]() 內種花,其余地方種草,且把種草的面積
內種花,其余地方種草,且把種草的面積![]() 與種花的面積
與種花的面積![]() 的比值
的比值![]() 稱為“草花比
稱為“草花比![]() ”.
”.
(Ⅰ)設![]() ,將
,將![]() 表示成
表示成![]() 的函數關系式;
的函數關系式;
(Ⅱ)當![]() 為多長時,
為多長時,![]() 有最小值?最小值是多少?
有最小值?最小值是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
(09年泗陽中學模擬六)(14分)
已知函數f(x)=![]() 為偶函數,且函數y=f(x)圖象的兩相鄰對稱軸間的距離為
為偶函數,且函數y=f(x)圖象的兩相鄰對稱軸間的距離為![]()
(Ⅰ)求f(![]() )的值;
)的值;
(Ⅱ)將函數y=f(x)的圖象向右平移![]() 個單位后,再將得到的圖象上各點的橫坐標舒暢長到原來的4倍,縱坐標不變,得到函數y=g(x)的圖象,求g(x)的單調遞減區間.
個單位后,再將得到的圖象上各點的橫坐標舒暢長到原來的4倍,縱坐標不變,得到函數y=g(x)的圖象,求g(x)的單調遞減區間.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com