
設(shè)函數(shù)f(x)=Asin(ωx+φ)(其中A>0,ω>0,-π<φ≤π)在x= 處取得最大值2,其圖象與x軸的相鄰兩個(gè)交點(diǎn)的距離為
處取得最大值2,其圖象與x軸的相鄰兩個(gè)交點(diǎn)的距離為 .
.
(1)求f(x)的解析式;
(2)求函數(shù)g(x)= 的值域.
的值域.
 應(yīng)用題點(diǎn)撥系列答案
應(yīng)用題點(diǎn)撥系列答案 狀元及第系列答案
狀元及第系列答案 同步奧數(shù)系列答案
同步奧數(shù)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源:2014年高考數(shù)學(xué)(理)二輪專(zhuān)題復(fù)習(xí)知能提升演練1-6-1練習(xí)卷(解析版) 題型:選擇題
已知圓(x-a)2+(y-b)2=r2的圓心為拋物線y2=4x的焦點(diǎn),且與直線3x+4y+2=0相切,則該圓的方程為( ).
A.(x-1)2+y2= B.x2+(y-1)2=
B.x2+(y-1)2=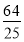
C.(x-1)2+y2=1 D.x2+(y-1)2=1
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2014年高考數(shù)學(xué)(理)二輪專(zhuān)題復(fù)習(xí)知能提升演練1-4-2練習(xí)卷(解析版) 題型:填空題
數(shù)列{an}的通項(xiàng)公式an=ncos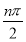 +1,前n項(xiàng)和為Sn,則S2 012=________.
+1,前n項(xiàng)和為Sn,則S2 012=________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2014年高考數(shù)學(xué)(理)二輪專(zhuān)題復(fù)習(xí)知能提升演練1-4-1練習(xí)卷(解析版) 題型:選擇題
在等差數(shù)列{an}中,a1+a5=10,a4=7,則數(shù)列{an}的公差為( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2014年高考數(shù)學(xué)(理)二輪專(zhuān)題復(fù)習(xí)知能提升演練1-3-2練習(xí)卷(解析版) 題型:選擇題
在△ABC中,∠ABC= ,AB=
,AB=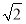 ,BC=3,則sin ∠BAC=( ).
,BC=3,則sin ∠BAC=( ).
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2014年高考數(shù)學(xué)(理)二輪專(zhuān)題復(fù)習(xí)知能提升演練1-3-1練習(xí)卷(解析版) 題型:填空題
函數(shù)f(x)=sin xcos x+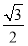 cos 2x的最小正周期T=________,振幅A=________.
cos 2x的最小正周期T=________,振幅A=________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2014年高考數(shù)學(xué)(理)二輪專(zhuān)題復(fù)習(xí)知能提升演練1-2-3練習(xí)卷(解析版) 題型:解答題
已知函數(shù)f(x)=ex(ax+b)-x2-4x,曲線y=f(x)在點(diǎn)(0,f(0))處的切線方程為y=4x+4.
(1)求a,b的值;
(2)討論f(x)的單調(diào)性,并求f(x)的極大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2014年高考數(shù)學(xué)(理)二輪專(zhuān)題復(fù)習(xí)知能提升演練1-2-2練習(xí)卷(解析版) 題型:選擇題
已知函數(shù)f(x)= x-log3x,若實(shí)數(shù)x0是方程f(x)=0的解,且0<x1<x0,則f(x1)的值 ( ).
x-log3x,若實(shí)數(shù)x0是方程f(x)=0的解,且0<x1<x0,則f(x1)的值 ( ).
A.恒為負(fù) B.等于零 C.恒為正 D.不大于零
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2014年高考數(shù)學(xué)(理)二輪專(zhuān)題復(fù)習(xí)知能提升演練1-1-1練習(xí)卷(解析版) 題型:選擇題
下列命題中,真命題是( ).
A.?x0∈R,ex0≤0
B.?x∈R,2x>x2
C.a+b=0的充要條件是 =-1
=-1
D.a>1,b>1是ab>1的充分條件
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com