
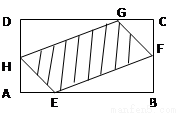
(本題滿分10分) 如圖,有一塊矩形空地,要在這塊空地上辟一個(gè)內(nèi)接四邊形為綠地,使其四個(gè)頂點(diǎn)分別落在矩形的四條邊上,已知AB=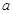 (
(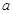 >2),BC=2,且AE=AH=CF=CG,
>2),BC=2,且AE=AH=CF=CG,
設(shè)AE=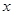 ,綠地面積為
,綠地面積為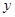 .
.
(1)寫出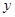 關(guān)于
關(guān)于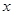 的函數(shù)關(guān)系式,并指出這個(gè)函數(shù)的定義域;
的函數(shù)關(guān)系式,并指出這個(gè)函數(shù)的定義域;
(2)當(dāng)AE為何值時(shí),綠地面積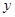 最大?
最大?
(1)SΔAEH=SΔCFG=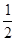 x2, SΔBEF=SΔDGH=
x2, SΔBEF=SΔDGH=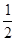 (
( -x)(2-x)
-x)(2-x)
∴y=SABCD-2SΔAEH-2SΔBEF=2 -x2-(
-x2-( -x)(2-x)=-2x2+(
-x)(2-x)=-2x2+( +2)x
+2)x
∴y=-2x2+( +2)x,0<x≤2
+2)x,0<x≤2
(2)當(dāng)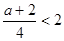 ,即
,即 <6時(shí),則x=
<6時(shí),則x=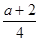 時(shí),y取最大值
時(shí),y取最大值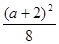
當(dāng)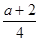 ≥2,即
≥2,即 ≥6時(shí),y=-2x2+(
≥6時(shí),y=-2x2+( +2)x,在
+2)x,在 0,2]上是增函數(shù),
0,2]上是增函數(shù),
則x=2時(shí),y取最大值2 -4
-4
綜上所述:當(dāng) <6時(shí),AE=
<6時(shí),AE=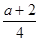 時(shí),綠地面積取最大值
時(shí),綠地面積取最大值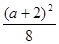
當(dāng) ≥6時(shí),AE=2時(shí),綠地面積取最大值2
≥6時(shí),AE=2時(shí),綠地面積取最大值2 -4
-4
【解析】本題主要考查實(shí)際問題中的建模和解模能力,注意二次函數(shù)求最值的方法.
(1)先求得四邊形ABCD,△AHE的面積,再分割法求得四邊形EFGH的面積,即建立y關(guān)于x的函數(shù)關(guān)系式;
(2)由(1)知y是關(guān)于x的二次函數(shù),用二次函數(shù)求最值的方法求解.
(1)SΔAEH=SΔCFG=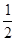 x2, SΔBEF=SΔDGH=
x2, SΔBEF=SΔDGH=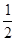 (
( -x)(2-x)
-x)(2-x)
∴y=SABCD-2SΔAEH-2SΔBEF=2 -x2-(
-x2-( -x)(2-x)=-2x2+(
-x)(2-x)=-2x2+( +2)x
+2)x
∴y=-2x2+( +2)x,0<x≤2
+2)x,0<x≤2
(2)當(dāng)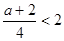 ,即
,即 <6時(shí),則x=
<6時(shí),則x=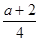 時(shí),y取最大值
時(shí),y取最大值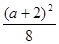
當(dāng)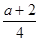 ≥2,即
≥2,即 ≥6時(shí),y=-2x2+(
≥6時(shí),y=-2x2+( +2)x,在
+2)x,在 0,2]上是增函數(shù),
0,2]上是增函數(shù),
則x=2時(shí),y取最大值2 -4
-4
綜上所述:當(dāng) <6時(shí),AE=
<6時(shí),AE=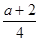 時(shí),綠地面積取最大值
時(shí),綠地面積取最大值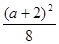
當(dāng) ≥6時(shí),AE=2時(shí),綠地面積取最大值2
≥6時(shí),AE=2時(shí),綠地面積取最大值2 -4
-4


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
17.本題滿分10分已知函數(shù)![]() 的圖象在y軸上的截距為
的圖象在y軸上的截距為![]() ,相鄰的兩個(gè)最值點(diǎn)是
,相鄰的兩個(gè)最值點(diǎn)是![]() 和
和![]() (1)求函數(shù)
(1)求函數(shù)![]() ;(2)設(shè)
;(2)設(shè)![]() ,問將函數(shù)
,問將函數(shù)![]() 的圖像經(jīng)過怎樣的變換可以得到
的圖像經(jīng)過怎樣的變換可以得到![]() 的圖像?(3)畫出函數(shù)
的圖像?(3)畫出函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的簡(jiǎn)圖.
上的簡(jiǎn)圖.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014屆浙江省高二下學(xué)期期中考試?yán)砜茢?shù)學(xué)試卷(解析版) 題型:解答題
(本題滿分10分)
(Ⅰ)設(shè) ,求證:
,求證: ;
;
(Ⅱ)設(shè) ,求證:三數(shù)
,求證:三數(shù) ,
, ,
, 中至少有一個(gè)不小于2.
中至少有一個(gè)不小于2.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014屆河南省高二上學(xué)期期末考試?yán)砜茢?shù)學(xué)試卷(解析版) 題型:解答題
(本題滿分10分)
如圖,已知正四棱柱ABCD—A1B1C1D1中,底面邊長(zhǎng)AB=2,側(cè)棱BB1的長(zhǎng)為4,過點(diǎn)B作B1C的垂線交側(cè)棱CC1于點(diǎn)E,交B1C于點(diǎn)F,

⑴求證:A1C⊥平面BDE;
⑵求A1B與平面BDE所成角的正弦值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年江蘇省揚(yáng)州市寶應(yīng)縣高三下學(xué)期期初測(cè)試數(shù)學(xué)試卷 題型:解答題
(本題滿分10分)
如圖,已知正三棱柱 的所有棱長(zhǎng)都為2,
的所有棱長(zhǎng)都為2, 為棱
為棱 的中點(diǎn),
的中點(diǎn),
(1)求證: 平面
平面 ;
;
(2)求二面角 的余弦值大小.
的余弦值大小.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011年遼寧省高二上學(xué)期期末考試數(shù)學(xué)理卷 題型:解答題
(本題滿分10分)
如圖,要計(jì)算西湖岸邊兩景點(diǎn) 與
與 的距離,由于地形的限制,需要在岸上選取
的距離,由于地形的限制,需要在岸上選取 和
和 兩點(diǎn),現(xiàn)測(cè)得
兩點(diǎn),現(xiàn)測(cè)得 ,
, ,
, ,
, ,
, ,求兩景點(diǎn)
,求兩景點(diǎn) 與
與 的距離(精確到0.1km).參考數(shù)據(jù):
的距離(精確到0.1km).參考數(shù)據(jù):
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com