
(本小題滿分12分)已知A、B、C為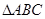 的三個內角且向量
的三個內角且向量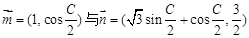 共線。
共線。
(Ⅰ)求角C的大小:
(Ⅱ)設角 的對邊分別是
的對邊分別是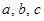 ,且滿足
,且滿足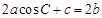 ,試判斷
,試判斷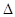
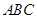 的形狀.
的形狀.
(1)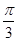 (2)△
(2)△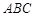 為等邊三角形
為等邊三角形
解析試題分析:(Ⅰ)(Ⅰ)∵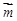 與
與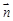 共線
共線
∴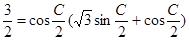
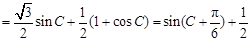 …………………………3分
…………………………3分
得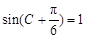 …………………………4分
…………………………4分
∴C=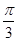 ……………………………6分
……………………………6分
(Ⅱ)方法1:由已知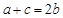 (1)
(1)
根據余弦定理可得: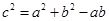 (2)……………………8分
(2)……………………8分
(1)、(2)聯立解得: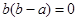 ……………………………10分
……………………………10分 為等邊三角形,……………………………12分
為等邊三角形,……………………………12分
方法2:
由正弦定理得: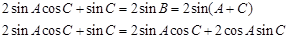 ……………………8分
……………………8分
∴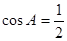 , ∴在△
, ∴在△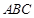 中 ∠
中 ∠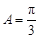 . ……………………………10分
. ……………………………10分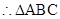 為等邊三角形 ……………………………12分
為等邊三角形 ……………………………12分
方法3:由(Ⅰ)知C=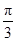 ,又由題設得:
,又由題設得: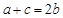 ,
,
在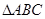 中根據射影定理得:
中根據射影定理得: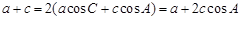 ……………………8分
……………………8分 ……………………………10分
……………………………10分
又. C=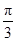 , 所以 △
, 所以 △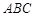 為等邊三角形, ……………………………12分
為等邊三角形, ……………………………12分
考點:考查了解三角形運用。
點評:解決該試題的關鍵是對于向量共線以及兩角和差的三角關系式的變形求解,同時能結合三角形的兩個定理來確定形狀,屬于基礎題。


 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com