（本題滿分12分）已知向量
，
.
（1）求
和
；
（2）當
為何值時，
．
閱讀快車系列答案科目：高中數學 來源： 題型：解答題
（本小題滿分12分）
已知向量
與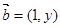
共線，且有函數
（Ⅰ）求函數的周期與最大值；
（Ⅱ）已知銳角DABC的三個內角分別是A、B、C，若有
，邊
，
，求AC的長.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（本小題滿分13分）
已知
, 
是平面上一動點, 到直線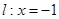
上的射影為點
，且滿足
（Ⅰ）求點的軌跡
的方程；
（Ⅱ）過點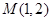
作曲線的兩條弦
, 設所在直線的斜率分別為
, 當變化且滿足
時，證明直線
恒過定點，并求出該定點坐標．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，
．（2）
.
，
，
， 
， 
， 
，
。
，
；（2）若
為單位向量，求
，
，函數
的單調遞增區間；
中，
分別是角
的對邊，且
，
，
，且
，求
的值．
中，
為
的中點，
分別在
上，且
,求
的值。
，
，若
為滿足
的一隨機整數，則
是直角三角形的概率為（ ）
，
，則
（ ）
滿足
，若
，
且
滿足：
，
，
為
。