中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

已知2×2矩陣M=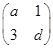有特征值λ=-1及對應的一個特征向量e1=.
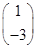(1)求矩陣M.
(2)設曲線C在矩陣M的作用下得到的方程為x2+2y2=1,求曲線C的方程.

(1)   (2) 22x2+4xy+y2=1

解析

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：填空題

已知當時，函數的最小值為-4，則t的取值范圍是       

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

求矩陣N＝的特征值及相應的特征向量．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

二階矩陣M對應變換將(1，－1)與(－2，1)分別變換成(5，7)與(－3，6)．
(1)求矩陣M；
(2)若直線l在此變換下所變換成的直線的解析式l′：11x－3y－68＝0，求直線l的方程．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

已知矩陣，，計算．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

已知△ABC,A(-1,0),B(3,0),C(2,1),對它先作關于x軸的反射變換,再將所得圖形繞原點逆時針旋轉90°.
(1)分別求兩次變換所對應的矩陣M1,M2.
(2)求△ABC在兩次連續的變換作用下所得到的△A'B'C'的面積.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

設M是把坐標平面上的點的橫坐標伸長到2倍，縱坐標伸長到3倍的伸壓變換．
(1)求矩陣M的特征值及相應的特征向量；
(2)求逆矩陣M－1以及橢圓＝1在M－1的作用下的新曲線的方程．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

變換對應的變換矩陣是
(1)求點在作用下的點的坐標；
(2)求函數的圖象在變換的作用下所得曲線的方程.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

點(－1，k)在伸壓變換矩陣之下的對應點的坐標為(－2，－4)，求m、k的值．

查看答案和解析>>

同步練習冊答案