中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

13．若的值為 , 14．以橢圓的右焦點(diǎn)為圓心.且與雙曲線的漸近線相切的圓的方程為 , 【查看更多】

 

題目列表(包括答案和解析)

(本小題滿分14分)

設(shè)橢圓的左、右焦點(diǎn)分別為F1、F2，上頂點(diǎn)為A，離心率e＝，在x軸負(fù)半軸上有一點(diǎn)B，且．

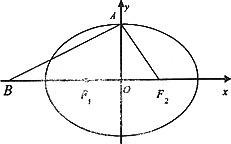
(Ⅰ)若過A、B、F2三點(diǎn)的圓恰好與直線相切，求橢圓C的方程；

(Ⅱ)在(Ⅰ)的條件下，過右焦點(diǎn)F2作斜率為k的直線與橢圓C交于M、N兩點(diǎn)，在x軸上是否存在點(diǎn)p(m，0)，使得以PM，PN為鄰邊的平行四邊形是菱形，如果存在，求出m的取值范圍；如果不存在，說明理由．

查看答案和解析>>

（2008•湖北模擬）橢圓C：
x2
a2
+
y2
b2
=1(a＞b＞0)的離心率為
6
3
，右準(zhǔn)線方程為x=
3
2
2
，左、右焦點(diǎn)分別為F1，F(xiàn)2．
（Ⅰ）求橢圓C的方程
（Ⅱ）若直線l：y=kx+t（t＞0）與以F1F2為直徑的圓相切，并與橢圓C交于A，B兩點(diǎn)，向量
AB
|
AB
|
在向量
F1F
2方向上的投影是p，且(
OA
•
OB
)p2=m（O為坐標(biāo)原點(diǎn)），求m與k的關(guān)系式；
（Ⅲ）在（Ⅱ）情形下，當(dāng)m∈[
1
4
，
1
2
]時，求△ABC面積的取值范圍．

查看答案和解析>>

（本題14分）已知橢圓的中心在坐標(biāo)原點(diǎn)，焦點(diǎn)在軸上，短軸長為2，且兩個焦點(diǎn)和短軸的兩個端點(diǎn)恰為一個正方形的頂點(diǎn)．過右焦點(diǎn)與軸不垂直的直線交橢圓于，兩點(diǎn)．

（Ⅰ）求橢圓的方程；

（Ⅱ）當(dāng)直線的斜率為1時，求的面積；

（Ⅲ）在線段上是否存在點(diǎn),使得以為鄰邊的平行四邊形是菱形？

若存在，求出的取值范圍；若不存在，請說明理由.

查看答案和解析>>

（本小題滿分14分）（注意：在試題卷上作答無效）

已知橢圓的左、右焦點(diǎn)分別為，若以為圓心，為半徑作圓，過橢圓上一點(diǎn)作此圓的切線，切點(diǎn)為，且的最小值不小于為．

（1）求橢圓的離心率的取值范圍；

（2）設(shè)橢圓的短半軸長為，圓與軸的右交點(diǎn)為，過點(diǎn)作斜率為的直線與橢圓相交于兩點(diǎn)，若，求直線被圓截得的弦長的最大值．

 

 

查看答案和解析>>

（本小題滿分14分）（注意：在試題卷上作答無效）
已知橢圓的左、右焦點(diǎn)分別為，若以為圓心，為半徑作圓，過橢圓上一點(diǎn)作此圓的切線，切點(diǎn)為，且的最小值不小于為．
（1）求橢圓的離心率的取值范圍；
（2）設(shè)橢圓的短半軸長為，圓與軸的右交點(diǎn)為，過點(diǎn)作斜率為的直線與橢圓相交于兩點(diǎn)，若，求直線被圓截得的弦長的最大值．

查看答案和解析>>


同步練習(xí)冊答案