中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

15．在等差數列中.滿足3a4=7a7.且a1>0.Sn是數列的前n項和.若Sn取得最大值.則n= . 【查看更多】

 

題目列表(包括答案和解析)

在等差數列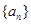中，.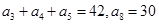

（1）求數列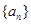的通項公式；

（2）若數列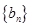滿足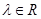（），則是否存在這樣的實數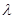使得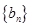為等比數列；

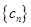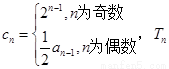（3）數列滿足為數列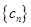的前n項和，求.

 

查看答案和解析>>

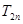在等差數列{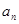}中，=3，其前項和為，等比數列{}的各項均為正數，=1，公比為q,且b2+ S2=12，．

（1）求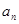與的通項公式；

（2）設數列{}滿足，求{}的前n項和．

 

查看答案和解析>>

（08年楊浦區測試）在等差數列中，公差，且，

（1）求的值．

   （2）當時，在數列中是否存在一項（正整數），使得  ， ，成等比數列，若存在，求的值；若不存在，說明理由．

（3）若自然數(為正整數)

滿足< <<  < <， 使得成等比數列，

   （文科考生做）當時，  用表示 ．　

   （理科考生做）求的所有可能值．

查看答案和解析>>

（2013•牡丹江一模）下列命題中，正確的是
（1）（2）（3）
（1）（2）（3）

（1）平面向量
a
與
b
的夾角為60°，
a
=(2，0)，|
b
|=1，則|
a
+
b
|=
7

（2）在△ABC中，A，B，C的對邊分別為a，b，c，若acosC，bcosB，ccosA成等差數列則B=
π
3

（3）O是△ABC所在平面上一定點，動點P滿足：
OP
=
OA
+λ(
AB
sinC
+
AC
sinB
)，λ∈（0，+∞），則直線AP一定通過△ABC的內心
（4）設函數f（x）=
x-[x]，x≥0
f(x+1)，x＜0
其中[x]表示不超過x的最大整數，如[-1.3]=-2，[1.3]=1，則函數y=f（x）-
1
4
x-
1
4
不同零點的個數2個．

查看答案和解析>>

若數列{an}的前n項和為Sn，且滿足等式an+2Sn=3．
（1）能否在數列中找到按原來順序成等差數列的任意三項，說明理由；
（2）能否從數列中依次抽取一個無限多項的等比數列，且使它的所有項和S滿足
9
160
＜S＜
1
13
，如果這樣的數列存在，這樣的等比數列有多少個？

查看答案和解析>>


同步練習冊答案