
題目列表(包括答案和解析)
3.排序
排序的算法很多,課本主要介紹里兩種排序方法:直接插入排序和冒泡排序
(1)直接插入排序
在日常生活中,經常碰到這樣一類排序問題:把新的數據插入到已經排好順序的數據列中。
例如:一組從小到大排好順序的數據列{1,3,5,7,9,11,13},通常稱之為有序列,我們用序號1,2,3,……表示數據的位置,欲把一個新的數據8插入到上述序列中。
完成這個工作要考慮兩個問題:
(1)確定數據“8”在原有序列中應該占有的位置序號。數據“8”所處的位置應滿足小于或等于原有序列右邊所有的數據,大于其左邊位置上所有的數據。
(2)將這個位置空出來,將數據“8”插進去。
對于一列無序的數據列,例如:{49,38,65,97,76,13,27,49},如何使用這種方法進行排序呢?基本思想很簡單,即反復使用上述方法排序,由序列的長度不斷增加,一直到完成整個無序列就有序了
首先,{49}是有序列,我們將38插入到有序列{49}中,得到兩個數據的有序列:
{38,49},
然后,將第三個數據65插入到上述序列中,得到有序列:
{38,49,65}
…………
按照這種方法,直到將最后一個數據65插入到上述有序列中,得到
{13,27,38,49,49,65,76,97}
這樣,就完成了整個數據列的排序工作。注意到無序列“插入排序算法”成為了解決這類問題的平臺
(2)冒泡法排序
所謂冒泡法排序,形象地說,就是將一組數據按照從小到大的順序排列時,小的數據視為質量輕的,大的數據視為質量沉的。一個小的數據就好比水中的氣泡,往上移動,一個較大的數據就好比石頭,往下移動。顯然最終會沉到水底,最輕的會浮到頂,反復進行,直到數據列排成為有序列。以上過程反映了這種排序方法的基本思路。
我們先對一組數據進行分析。
設待排序的數據為:{49,38,65,97,76,13,27,49}
排序的具體操作步驟如下:
2.秦九韶算法
秦九韶算法的一般規則:
秦九韶算法適用一般的多項式f(x)=anxn+an-1xn-1+….+a1x+a0的求值問題。用秦九韶算法求一般多項式f(x)= anxn+an-1xn-1+….+a1x+a0當x=x0時的函數值,可把n次多項式的求值問題轉化成求n個一次多項式的值的問題,即求
v0=an
v1=anx+an-1
v2=v1x+an-2
v3=v2x+an-3
……..
vn=vn-1x+a0
觀察秦九韶算法的數學模型,計算vk時要用到vk-1的值,若令v0=an。
我們可以得到下面的遞推公式:
v0=an
vk=vk-1+an-k(k=1,2,…n)
這是一個在秦九韶算法中反復執行的步驟,可以用循環結構來實現
1.求最大公約數
(1)短除法
求兩個正整數的最大公約數的步驟:先用兩個數公有的質因數連續去除,一直除到所得的商是兩個互質數為止,然后把所有的除數連乘起來
(2)窮舉法(也叫枚舉法)
窮舉法求兩個正整數的最大公約數的解題步驟:從兩個數中較小數開始由大到小列舉,直到找到公約數立即中斷列舉,得到的公約數便是最大公約數

(3)輾轉相除法
輾轉相除法求兩個數的最大公約數,其算法可以描述如下:
① 輸入兩個正整數m和n;
② 求余數r:計算m除以n,將所得余數存放到變量r中;
③更新被除數和余數:m=n,n=r;
④判斷余數r是否為0。若余數為0,則輸出結果;否則轉向第②步繼續循環執行
如此循環,直到得到結果為止。
(4)更相減損術
我國早期也有解決求最大公約數問題的算法,就是更相減損術。在《九章算術》中記載了更相減損術求最大公約數的步驟:可半者半之,不可半者,副置分母•子之數,以少減多,更相減損,求其等也,以等數約之
步驟:
Ⅰ.任意給出兩個正數;判斷它們是否都是偶數。若是,用2約簡;若不是,執行第二步。
Ⅱ.以較大的數減去較小的數,接著把較小的數與所得的差比較,并以大數減小數。繼續這操作,直到所得的數相等為止,則這個數(等數)就是所求的最大公約數。
算法是高中數學新課程中的新增內容,本講的重點是幾種重要的算法案例思想,復習時重算法的思想輕算法和程序的構造。
預測2010年高考隊本講的考察是:以選擇題或填空題的形式出現,分值在5分左右,考察的熱點是算法實例和傳統數學知識的結合題目
32.(湖北卷)某單位最近組織了一次健身活動,活動分為登山組和游泳組,且每個職工至多參加了其中一組。在參加活動的職工中,青年人占42.5%,中年人占47.5%,老年人占10%。登山組的職工占參加活動總人數的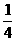 ,且該組中,青年人占50%,中年人占40%,老年人占10%。為了了解各組不同的年齡層次的職工對本次活動的滿意程度,現用分層抽樣的方法從參加活動的全體職工中抽取一個容量為200的樣本。試確定
,且該組中,青年人占50%,中年人占40%,老年人占10%。為了了解各組不同的年齡層次的職工對本次活動的滿意程度,現用分層抽樣的方法從參加活動的全體職工中抽取一個容量為200的樣本。試確定
(1)游泳組中,青年人、中年人、老年人分別所占的比例;
(2)游泳組中,青年人、中年人、老年人分別應抽取的人數
本小題主要考查分層抽樣的概念和運算,以及運用統計知識解決實際問題的能力.
解 (1)設登山組人數為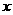 ,游泳組中,青年人、中年人、老年人各占比例分別為a、b、c,則有
,游泳組中,青年人、中年人、老年人各占比例分別為a、b、c,則有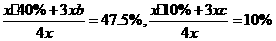 ,解得b=50%,c=10%.
,解得b=50%,c=10%.
故a=100%-50%-10%=40%,即游泳組中,青年人、中年人、老年人各占比例分別為40%、
50%、10%。
(2)游泳組中,抽取的青年人數為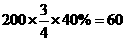 (人);抽取的中年人數為
(人);抽取的中年人數為
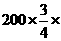 50%=75(人);抽取的老年人數為
50%=75(人);抽取的老年人數為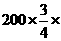 10%=15(人)
10%=15(人)
0.7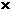 100+0.35=70.35
100+0.35=70.35
故耗能減少了90-70.35=19.65(噸)
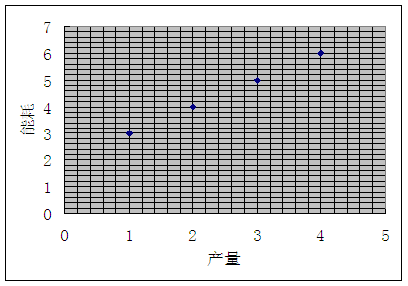
30.(2007廣東理)下表提供了某廠節能降耗技術改造后生產甲產品過程中記錄的產量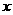 (噸)與相應的生產能耗
(噸)與相應的生產能耗 (噸標準煤)的幾組對照數據
(噸標準煤)的幾組對照數據
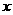
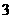
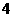
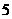
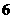

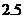
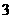
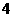
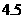
(1)請畫出上表數據的散點圖;
(2)請根據上表提供的數據,用最小二乘法求出 關于
關于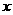 的線性回歸方程
的線性回歸方程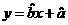 ;
;
(3)已知該廠技改前100噸甲產品的生產能耗為90噸標準煤.試根據(2)求出的線性
回歸方程,預測生產100噸甲產品的生產能耗比技改前降低多少噸標準煤?
(參考數值: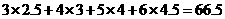 )
)
解 (1)如下圖
(2)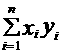 =3
=3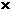 2.5+4
2.5+4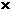 3+5
3+5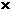 4+6
4+6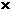 4.5=66.5
4.5=66.5
 =
=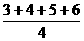 =4.5
=4.5
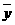 =
= =3.5
=3.5
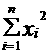 =
=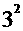 +
+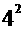 +
+ +
+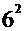 =86
=86
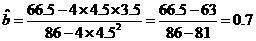
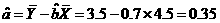
故線性回歸方程為y=0.7x+0.35
(3)根據回歸方程的預測,現在生產100噸產品消耗的標準煤的數量為
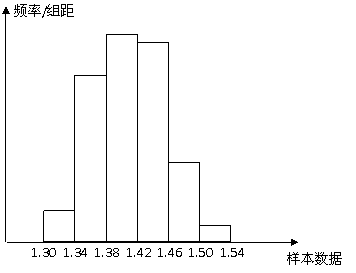
28.(2007湖南文)(本小題滿分12分)在生產過程中,測得纖維產品的纖度(表示纖維粗細的一種量)共有100個數據,將數據分組如右表:
(1)在答題卡上完成頻率分布表,并在給定的坐標系中畫出頻率分布直方圖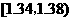 ;
;
(2)估計纖度落在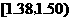 中的概率及纖度小于
中的概率及纖度小于 的概率是多少?
的概率是多少?
(3)統計方法中,同一組數據常用該組區間的中點值(例如區間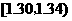 的中點值
的中點值
是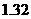 )作為代表.據此,估計纖度的期望.
)作為代表.據此,估計纖度的期望.
|
分組 |
頻數 |
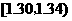 |
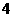 |
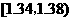 |
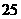 |
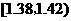 |
 |
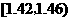 |
 |
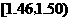 |
 |
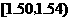 |
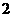 |
|
合計 |
 |
解 (Ⅰ)
|
分組 |
頻數 |
頻率 |
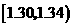 |
4 |
0.04 |
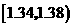 |
25 |
0.25 |
 |
30 |
0.30 |
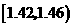 |
29 |
0.29 |
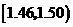 |
10 |
0.10 |
|
|
2 |
0.02 |
|
合計 |
100 |
1.00 |
(Ⅱ)纖度落在 中的概率約為
中的概率約為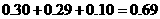 ,纖度小于1.40的概率約為
,纖度小于1.40的概率約為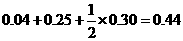 .
.
(Ⅲ)總體數據的期望約為
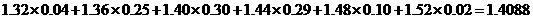
27.(2007湖南文)根據某水文觀測點的歷史統計數據,得到某條河流水位的頻率分布直方圖(如圖2).從圖中可以看出,該水文觀測點平均至少一百年才遇到一次的洪水的最低水位是 ( )
A.48米 B.49米 C.50米 D.51米


答案 C
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com