
題目列表(包括答案和解析)
2.設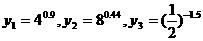 ,則 ( )
,則 ( )
A.y3>y1>y2 B.y2>y1>y3 C.y1>y2>y3 D.y1>y3>y2
1.設集合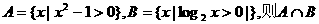 等于 ( )
等于 ( )
A.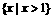 B.
B.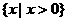
C.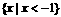 D.
D.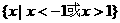
22. (1)如圖,k
(1)如圖,k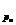 Q
Q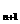 =
=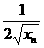 ,P
,P Q
Q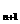 的方程為y-y
的方程為y-y =
=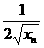 (x-x
(x-x ),
), y
y =
=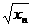 ,
, y-
y-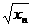 =
=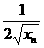 (x-x
(x-x )。令x=0,得y
)。令x=0,得y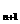 =
=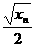 ,又P
,又P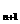 在y
在y =x
=x
上,y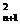 =x
=x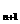 ,即(
,即(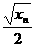 )
) = x
= x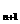
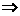
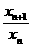 =
=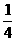 ,{ x
,{ x }是等比數
}是等比數
列,x =f(n)=(
=f(n)=(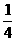 )
)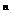 (其中n=0,1,2,…)。
(其中n=0,1,2,…)。
(2)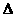 P
P Q
Q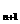 P
P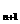 的面積記為S
的面積記為S ,則S
,則S =
= x
x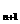 (y
(y -y
-y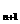 ),
),
而x =(
=(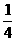 )
)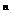 ,y
,y =
=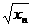 =(
=( )
)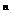 ,
, S
S =
= (
(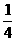 )
)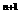 [(
[( )
)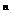 -(
-( )
)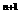 ]=(
]=( )
)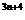 。{ S
。{ S }是首項為S
}是首項為S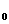 =(
=( )
)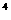 、公比為(
、公比為( )
)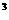 的無窮遞縮數列,
的無窮遞縮數列, S
S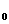 +S
+S +S
+S +…+ S
+…+ S +…=
+…=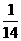
(3)| P P
P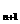 |=
|=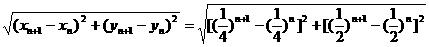 =
=
( )
)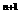
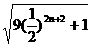 ,
, lim
lim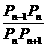 =2 lim
=2 lim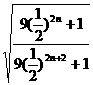 =2
=2
21.(1)依題意得,新建道路交叉口的總造價(單位:萬元)為y=k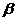 n=k
n=k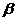 (ax+b)。
(ax+b)。
(2)P=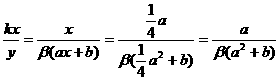 。
。
由于5﹪
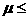 10﹪,有0.05
10﹪,有0.05
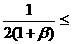 0.1。
0.1。
則0.1
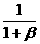
 0.2,
0.2, 0.05
0.05 1+
1+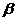
 10,
10, 4
4
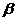
 9,
9,
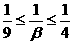 ,又由已知P>0,從而
,又由已知P>0,從而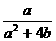 >0。
>0。
 P的取值范圍是
P的取值范圍是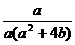
 P
P
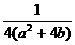 (無等號不扣分)
(無等號不扣分)
(3)當b=4時,在(2)的條件下,若路網最通暢,則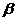 =9,又總造價比最高,
=9,又總造價比最高, P=
P=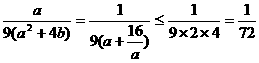 。
。
當且僅當a=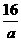 時,即a=4時取等號,
時,即a=4時取等號, 滿足(3)的條件的原有道路路標段是4個
滿足(3)的條件的原有道路路標段是4個
20.(1)x ,x
,x
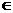 (0,1),且x
(0,1),且x <x
<x ,則f(x
,則f(x )-f(x
)-f(x )=-(x
)=-(x -x
-x )(x
)(x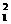 + x
+ x x
x +x
+x -a)<0,
-a)<0,
x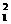 + x
+ x x
x +x
+x -a,a> x
-a,a> x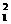 + x
+ x x
x +x
+x ,而x
,而x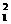 + x
+ x x
x +x
+x <(x
<(x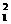 +x
+x )+
)+ (x
(x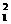 +x
+x )=
)=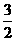 (x
(x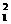 +x
+x )
)
<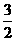 ×2=3,
×2=3, a
a 3。
3。
(2)當a=3時,a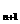 =-
=- a
a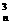 +
+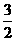 a
a 。下面用數學歸納法證明:0< a
。下面用數學歸納法證明:0< a <1。
<1。
當n=1時,a
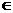 (0,1);
(0,1);
假設n = k時,a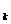
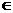 (0,1),則a
(0,1),則a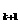 =
= a
a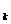 (3-a
(3-a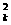 )>0,
)>0, f(x)在(0,1)上遞增,0< a
f(x)在(0,1)上遞增,0< a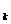 <1,
<1,
 a
a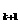 =
= a
a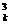 +
+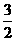 a
a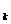 <-
<- ·1
·1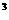 +
+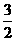 ·1=1。
·1=1。 0< a
0< a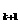 <1,即n =k+1時,也成立。
<1,即n =k+1時,也成立。 a
a
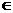 (0,1)。
(0,1)。
19.(1)若CD 平面PAD,則CD
平面PAD,則CD PD,由已知PC=PD,得
PD,由已知PC=PD,得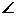 PCD=
PCD=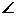 PDC<90°,這與CD
PDC<90°,這與CD PD矛盾,所以CD與平面QAD不垂直。
PD矛盾,所以CD與平面QAD不垂直。
(2)取AB、CD的中點E、F,聯結PE、PF、EF,由PA=PB,PC=PD,得PE AB,PF
AB,PF CD。
CD。 EF為直角梯形的中位線,EF
EF為直角梯形的中位線,EF CD,又PF
CD,又PF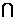 EF=F,
EF=F, CD
CD 平面PEF,由PE
平面PEF,由PE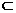 平面PEF,得CD
平面PEF,得CD PE,又AB
PE,又AB PE且梯形兩腰AB、CD必相交,
PE且梯形兩腰AB、CD必相交, PE
PE 平面ABCD,又PE
平面ABCD,又PE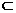 墻面PAB,平面PAB
墻面PAB,平面PAB 平面ABCD。
平面ABCD。
|
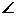 PFE為二面角P-CD-A的平面角,做EG
PFE為二面角P-CD-A的平面角,做EG BC于G,連PG,由三垂線定理得BC
BC于G,連PG,由三垂線定理得BC PG,故
PG,故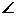 PGE為二面角P-CD-A的平面角,即
PGE為二面角P-CD-A的平面角,即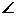 PGE=60°,由已知,得EF=
PGE=60°,由已知,得EF= (AD+BC)=
(AD+BC)= CD,又EG=CF=
CD,又EG=CF= CD。
CD。 EF=EG,易證得Rt
EF=EG,易證得Rt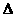 PEF = Rt
PEF = Rt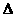 PEG。
PEG。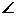 PFE=
PFE=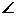 PGE=60°,即為所求。
PGE=60°,即為所求。18.(1)元件A正常工作的概率P(A)=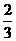 ,它不正常工作的概率P(
,它不正常工作的概率P(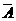 )=1-P(A)=
)=1-P(A)=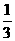 。
。
(2)元件A、B、C都正常工作的概率P(A·B·C)=P(A)·P(B)·P(C)=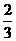 ·
·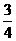 ·
·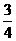 =
=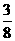 。
。
(3)系統N正常工作可分為A、B、C都正常工作和A、D正常工作但B、C不都正常工作兩種情況,
前者概率為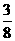 ,后者的概率為P(A·
,后者的概率為P(A·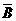 ·C·D)+P(A·B·
·C·D)+P(A·B·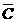 ·D)+P(A·
·D)+P(A·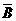 ·
·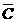 ·D)
·D)
=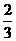 ·
·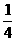 ·
·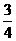 ·
·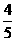 +
+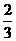 ·
·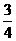 ·
·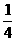 ·
·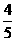 +
+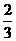 ·
·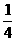 ·
·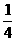 ·
·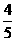 =
=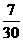 ,所以系統N正常工作的概率是
,所以系統N正常工作的概率是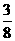 +
+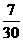 =
=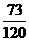 .
.
17.(1)f(-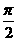 )= f(
)= f(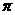 )=sin
)=sin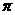 =0,f(-
=0,f(-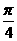 )= f(
)= f(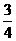
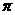 )=sin
)=sin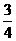
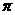 =
=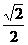
(2)當-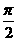
 x<
x<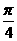 時,f(x)= f(
時,f(x)= f(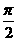 -x)=sin(
-x)=sin(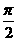 -x)=cos x
-x)=cos x  f(x)=
f(x)=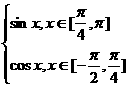
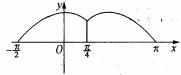 (3)做函數f(x)的圖象
(3)做函數f(x)的圖象
顯然,若f(x)=a有解,則a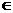 [0,1]
[0,1]
①0 a<
a<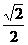 ,f(x)=a有兩解,M
,f(x)=a有兩解,M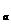 =
=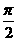 。
。
②a=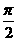 ,f(x)=a有三解,M
,f(x)=a有三解,M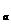 =
=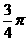 。
。
③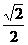 <a<1,f(x)=a有四解,M
<a<1,f(x)=a有四解,M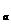 =
=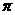 。
。
④a=1,f(x)=a有兩解,M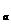 =
=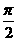 。
。
16.(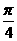 ,arctan4) S=
,arctan4) S= | OF | · | FQ |sin〈
| OF | · | FQ |sin〈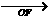 ·
·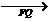 〉
〉
 ·
· =|
=| | · |
| · | | cos〈
| cos〈 ·
· 〉
〉  S=
S= tan〈
tan〈 ·
· 〉
〉

 <S<2,
<S<2,  1< tan〈
1< tan〈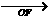 ·
·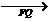 〉<4 又
〉<4 又
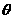
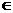 [0,
[0,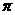 ]
] 
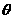
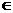 (
(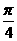 ,arctan4)
,arctan4)
15.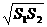
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com