
已知函數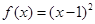 ,數列
,數列 是公差為d的等差數列,
是公差為d的等差數列,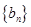 是公比為q(
是公比為q(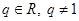 )的等比數列.若
)的等比數列.若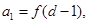
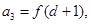

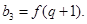
(Ⅰ)求數列 ,
,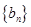 的通項公式;
的通項公式;
(Ⅱ)設數列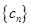 對任意自然數n均有
對任意自然數n均有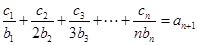 ,求
,求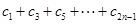 的值;
的值;
(Ⅲ)試比較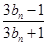 與
與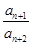 的大小.
的大小.
(1)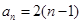 ,
, (2)
(2) (3)
(3)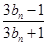
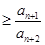
解析試題分析:(Ⅰ) ∵ 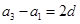 , ∴
, ∴ 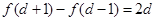 .
.
即 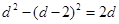 , 解得 d =2.
, 解得 d =2.
∴  . ∴
. ∴ 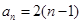 2分
2分
∵  , ∴
, ∴  .
.
∵  , ∴
, ∴  .
.
又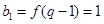 , ∴
, ∴  . 4分
. 4分
(Ⅱ) 由題設知  , ∴
, ∴ .
.
當 時,
時, 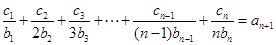 ,
, ,
,
兩式相減,得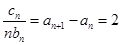 .
.
∴  (
( 適合). 7分
適合). 7分
設T=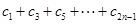 ,
,
∴ 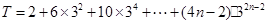
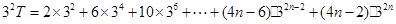
兩式相減 ,得 
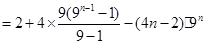
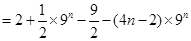
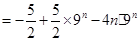 .
.
∴  . 10分
. 10分
(Ⅲ) 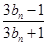
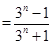
 ,
, 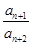
 .
.
現只須比較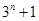 與
與 的大小.
的大小.
當n=1時, 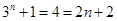 ;
;
當n=2時, 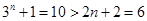 ;
;
當n=3時,  ;
;
當n=4時,  .
.
猜想 時,
時,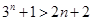 . 12分
. 12分
用數學歸納法證明
(1)當n=2時,左邊 ,右邊
,右邊 ,
,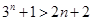 成立.
成立.
(2)假設當n=k時, 不等式成立,即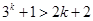 .
.
當n=k+1時, 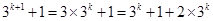

 .
.
即當n=k+1時,不等式也成立.
由(1)(2),可知 時,
時,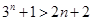 都成立.
都成立.
所以 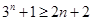 (當且僅當n=1時,等號成立)
(當且僅當n=1時,等號成立)
所以
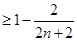 .即
.即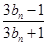
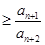 . 14分
. 14分
考點:等差數列和等比數列
點評:主要是考查了等差數列和等比數列的通項公式和求和運用,以及數學歸納法來猜想證明大小,屬于難度試題。


科目:高中數學 來源: 題型:解答題
設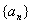 是各項都為正數的等比數列,
是各項都為正數的等比數列, 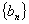 是等差數列,且
是等差數列,且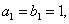 ,
,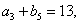
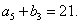
(1)求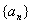 ,
,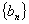 的通項公式;
的通項公式;
(2)記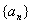 的前
的前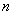 項和為
項和為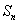 ,求證:
,求證: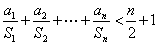 ;
;
(3)若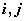 均為正整數,且
均為正整數,且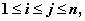 記所有可能乘積
記所有可能乘積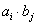 的和
的和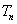 ,求證:
,求證: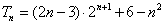 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com