
設橢圓的方程為 ,斜率為1的直線不經(jīng)過原點
,斜率為1的直線不經(jīng)過原點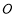 ,而且與橢圓相交于
,而且與橢圓相交于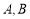 兩點,
兩點,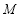 為線段
為線段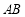 的中點.
的中點.
(1)問:直線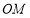 與
與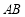 能否垂直?若能,
能否垂直?若能,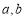 之間滿足什么關系;若不能,說明理由;
之間滿足什么關系;若不能,說明理由;
(2)已知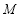 為
為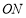 的中點,且
的中點,且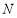 點在橢圓上.若
點在橢圓上.若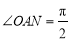 ,求橢圓的離心率.
,求橢圓的離心率.
(1)直線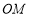 與
與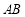 不能垂直;(2)
不能垂直;(2)
【解析】
試題分析:(1)設直線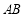 的方程為
的方程為 ,與橢圓方程聯(lián)立,消去
,與橢圓方程聯(lián)立,消去 整理為關于
整理為關于 的一元二次方程,因為有兩個交點則判別式應大于0,由韋達定理可得根與系數(shù)的關系,用中點坐標公式求點
的一元二次方程,因為有兩個交點則判別式應大于0,由韋達定理可得根與系數(shù)的關系,用中點坐標公式求點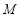 的坐標。求出直線
的坐標。求出直線 的斜率,假設兩直線垂直則斜率相乘等于
的斜率,假設兩直線垂直則斜率相乘等于 ,解出
,解出 的關系式,根據(jù)關系式及橢圓中
的關系式,根據(jù)關系式及橢圓中 的關系判斷假設成立與否。(2)∵M為ON的中點,M為AB的中點,∴四邊形OANB為平行四邊形.
的關系判斷假設成立與否。(2)∵M為ON的中點,M為AB的中點,∴四邊形OANB為平行四邊形.
∵ ,∴四邊形OANB為矩形,∴
,∴四邊形OANB為矩形,∴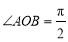 ,轉化為向量問題,可得
,轉化為向量問題,可得 的關系式。由中點坐標公式可得點
的關系式。由中點坐標公式可得點 的坐標,將其代入橢圓方程,與上式聯(lián)立消去
的坐標,將其代入橢圓方程,與上式聯(lián)立消去 即可得
即可得 之間滿足的關系式。將
之間滿足的關系式。將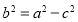 代入
代入 之間的關系式,可求其離心率。
之間的關系式,可求其離心率。
試題解析:解答:(1)∵斜率為1的直線不經(jīng)過原點 ,而且與橢圓相交于
,而且與橢圓相交于 兩點,
兩點,
∴可以設直線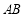 的方程為
的方程為 .
.
∵ ,∴
,∴ ,
,
∴ . ① 1分
. ① 1分
∵直線 與橢圓相交于
與橢圓相交于 兩點,∴
兩點,∴
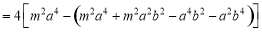
 . ② 2分
. ② 2分
且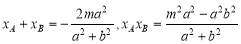 . ③ 3分
. ③ 3分
∵ 為線段
為線段 的中點,∴
的中點,∴ ,
,
∴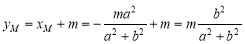 ,∴
,∴ . 4分
. 4分
假設直線 與
與 能垂直.
能垂直.
∵直線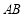 的斜率為1,∴直線
的斜率為1,∴直線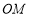 的斜率為-1,
的斜率為-1,
∴ ,∴
,∴ . 5分
. 5分
∵在橢圓方程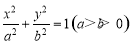 中,
中, ,
,
∴假設不正確,在橢圓中直線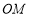 與
與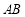 不能垂直. 6分
不能垂直. 6分
(2)∵M為ON的中點,M為AB的中點,∴四邊形OANB為平行四邊形.
∵ ,∴四邊形OANB為矩形,∴
,∴四邊形OANB為矩形,∴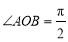 , 7分
, 7分
∴ ,∴
,∴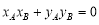 ,∴
,∴ ,
,
∴ ,
,
∴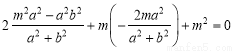 ,整理得
,整理得 . 8分
. 8分
∵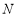 點在橢圓上,∴
點在橢圓上,∴ ,∴
,∴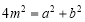 . 9分
. 9分
此時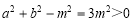 ,滿足
,滿足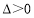 ,
,
消去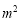 得
得 ,即
,即 . 10分
. 10分
設橢圓的離心率為e,則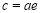 ,∴
,∴ ,
,
∴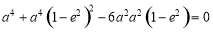 ,∴
,∴ ,
,
∴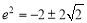 ,∵
,∵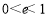 ,∴
,∴ .
.
考點:1直線與橢圓的位置關系;2直線垂直時斜率的關系;3轉化思想。


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案科目:高中數(shù)學 來源:2016屆北京市海淀區(qū)高一上學期期末統(tǒng)考數(shù)學試卷(解析版) 題型:選擇題
下列四個函數(shù)中,以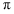 為最小正周期,且在區(qū)間
為最小正周期,且在區(qū)間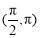 上為減函數(shù)的是( )
上為減函數(shù)的是( )
A.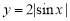 B.
B.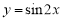 C.
C.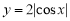 D.
D.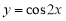
查看答案和解析>>
科目:高中數(shù)學 來源:2015屆重慶市高二上學期期末考試理科數(shù)學試卷(解析版) 題型:選擇題
已知雙曲線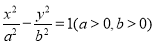 的右焦點為
的右焦點為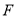 ,若過點
,若過點 且傾斜角為
且傾斜角為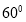 的直線與雙曲線的右支有且只有一個交點,則此雙曲線離心率的取值范圍是( )
的直線與雙曲線的右支有且只有一個交點,則此雙曲線離心率的取值范圍是( )
A.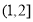 B.
B.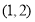 C.
C.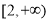 D.
D.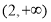
查看答案和解析>>
科目:高中數(shù)學 來源:2015屆遼寧省沈陽市高二質(zhì)量監(jiān)測理科數(shù)學試卷(解析版) 題型:選擇題
已知ABCD是四面體,且O為△BCD內(nèi)一點,則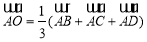 是O為△BCD的重心的 ( )
是O為△BCD的重心的 ( )
A.充分不必要條件 B.必要不充分條件
C.充要條件 D.既不充分又不必要條件
查看答案和解析>>
科目:高中數(shù)學 來源:2015屆遼寧省沈陽市高二質(zhì)量監(jiān)測文科數(shù)學試卷(解析版) 題型:填空題
在等差數(shù)列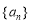 中,當
中,當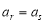
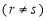 時,
時,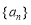 必定是常數(shù)數(shù)列. 然而在等比數(shù)列
必定是常數(shù)數(shù)列. 然而在等比數(shù)列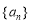 中,對某些正整數(shù)r、s
中,對某些正整數(shù)r、s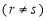 ,當
,當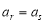 時,
時,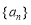 可以不是常數(shù)列,試寫出非常數(shù)數(shù)列
可以不是常數(shù)列,試寫出非常數(shù)數(shù)列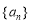 的一個通項公式 .
的一個通項公式 .
查看答案和解析>>
科目:高中數(shù)學 來源:2015屆遼寧大連普通高中高二上學期期末考試文數(shù)學卷(解析版) 題型:解答題
不等式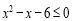 解集為
解集為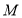 ,不等式
,不等式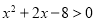 解集為
解集為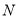 ,不等式
,不等式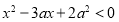
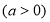 解集為
解集為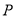 .
.
(1)求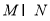 ;
;
(2)若“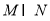 ”是“
”是“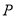 ”的充分條件,求實數(shù)
”的充分條件,求實數(shù)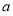 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com