
(本小題滿分12分)
在 中,
中,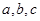 分別為內角
分別為內角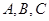 的對邊,且
的對邊,且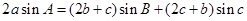 .
.
(1)求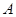
 的大小;
的大小;
(2)若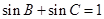 ,試判斷
,試判斷 的形狀;
的形狀;
(1) 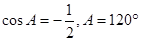 . (2)
. (2)  是等腰的鈍角三角形.
是等腰的鈍角三角形.
解析試題分析:(Ⅰ)利用正弦定理把題設等式中的角的正弦轉化成邊,求得a,b和c關系式,代入余弦定理中求得cosA的值,進而求得A.
(Ⅱ)把(Ⅰ)中a,b和c關系式利用正弦定理轉化成角的正弦,與sinB+sinC=1聯立求得sinB和sinC的值,進而根據C,B的范圍推斷出B=C,可知△ABC是等腰的鈍角三角形
(1)由已知,根據正弦定理得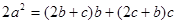 ,
,
即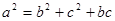 .
.
由余弦定理得 ,
,
故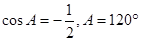 .……6分
.……6分
(2)由(1)得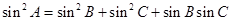 .
.
又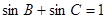 ,得
,得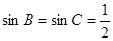 .
.
因為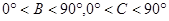 ,
,
故B=C.
所以 是等腰的鈍角三角形. …………12分考點:本題主要考查正弦定理和余弦定理的應用.
是等腰的鈍角三角形. …………12分考點:本題主要考查正弦定理和余弦定理的應用.
點評:解決該試題的關鍵是在解三角形問題中一般借助正弦定理和余弦定理邊化角,角化邊達到解題的目的.


科目:高中數學 來源: 題型:解答題
(本題滿分13 分)
據氣象部門預報,在距離某碼頭南偏東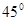 方向600km處的熱帶風暴中心,正以每小時20km的速度向正北方向移動,距風暴中心450km以內的地區都將受到影響,從現在起多長時間后,該碼頭將受到熱帶風暴中心的影響,影響多長時間?(精確到0.1h)
方向600km處的熱帶風暴中心,正以每小時20km的速度向正北方向移動,距風暴中心450km以內的地區都將受到影響,從現在起多長時間后,該碼頭將受到熱帶風暴中心的影響,影響多長時間?(精確到0.1h)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分13分)我炮兵陣地位于地面A處,兩觀察所分別位于地面點C和D處,已知CD=6 ,∠ACD=45°,∠ADC=75°, 目標出現于地面點B處時,測得∠BCD=30°,∠BDC=15°(如圖),求炮兵陣地到目標的距離.
,∠ACD=45°,∠ADC=75°, 目標出現于地面點B處時,測得∠BCD=30°,∠BDC=15°(如圖),求炮兵陣地到目標的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
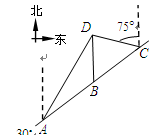
如圖,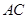 是佛山市一環東線的一段,其中
是佛山市一環東線的一段,其中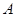 、
、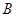 、
、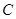 分別是林上路、佛陳路、花卉大道出口,經測量陳村花卉世界
分別是林上路、佛陳路、花卉大道出口,經測量陳村花卉世界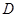 位于點
位于點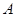 的北偏東
的北偏東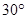 方向
方向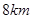 處,位于點
處,位于點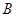 的正北方向,位于點
的正北方向,位于點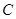 的北偏西
的北偏西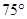 方向上,并且
方向上,并且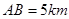 .
.
(1) 求佛陳路出口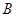 與花卉世界
與花卉世界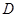 之間的距離;(精確到0.1km)
之間的距離;(精確到0.1km)
(2) 求花卉大道出口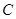 與花卉世界
與花卉世界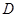 之間的距離.(精確到0.1km)
之間的距離.(精確到0.1km)
(參考數據: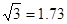 ,
,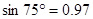 ,
,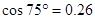 ,
,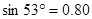 ,
,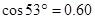 ,
, 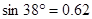 ,
,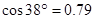
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com