
(本題滿分13分)我炮兵陣地位于地面A處,兩觀察所分別位于地面點(diǎn)C和D處,已知CD=6 ,∠ACD=45°,∠ADC=75°, 目標(biāo)出現(xiàn)于地面點(diǎn)B處時,測得∠BCD=30°,∠BDC=15°(如圖),求炮兵陣地到目標(biāo)的距離.
,∠ACD=45°,∠ADC=75°, 目標(biāo)出現(xiàn)于地面點(diǎn)B處時,測得∠BCD=30°,∠BDC=15°(如圖),求炮兵陣地到目標(biāo)的距離.
炮兵陣地到目標(biāo)的距離為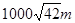 .
.
解析試題分析:在△ACD中,依題意可求得,∠CAD,利用正弦定理求得BD的長,進(jìn)而在△ABD中,利用勾股定理求得AB.
解:在△ACD中,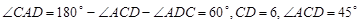
根據(jù)正弦定理有: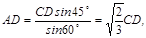
同理:在△BCD中,
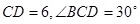 ,
,
根據(jù)正弦定理有: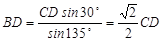 ,
,
在△ABD中,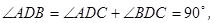 根據(jù)勾股定理有:
根據(jù)勾股定理有: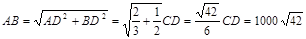 ,
,
所以炮兵陣地到目標(biāo)的距離為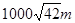 .………………………………13分
.………………………………13分
考點(diǎn):本試題主要考查了解三角形的實(shí)際應(yīng)用.利用了正弦定理和余弦整體定理,完成了邊角的問題的互化.
點(diǎn)評:解決該試題的關(guān)鍵是在△ACD中,利用正弦定理求得BD的長,在△ABD中,利用勾股定理求得AB.


 培優(yōu)口算題卡系列答案
培優(yōu)口算題卡系列答案 開心口算題卡系列答案
開心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
本小題滿分10分)設(shè)函數(shù)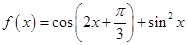 ,
,
(Ⅰ)求函數(shù)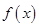 的最大值和最小正周期.,
的最大值和最小正周期.,
(Ⅱ)設(shè)A,B,C為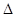 ABC的三個內(nèi)角,若
ABC的三個內(nèi)角,若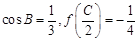 ,且C為銳角,求
,且C為銳角,求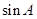
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題12分)
在銳角△ABC中,a、b、c分別為角A、B、C所對的邊,且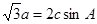
(1)求角C的大小;
(2)若c= ,且△ABC的面積為
,且△ABC的面積為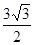
 ,求a+b的值。
,求a+b的值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
在△ABC中,角A,B,C所對的邊分別為a,b,c,設(shè)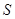 為△ABC的面積,滿足
為△ABC的面積,滿足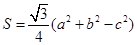 .(1)求角C的大小;(2)求
.(1)求角C的大小;(2)求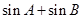 的最大值.
的最大值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com