中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

本小題滿分10分）設函數，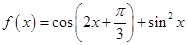
（Ⅰ）求函數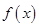的最大值和最小正周期.，
（Ⅱ）設A,B,C為ABC的三個內角，若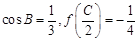，且C為銳角，求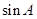

（1）f(x)的最大值為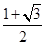,最小正周期.
（2）

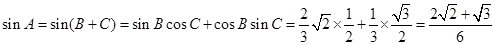
解析試題分析：（1）首先利用二倍角公式化為單一函數，求解最值。
（2）在第一問的基礎上，進一步利用同角關系得到B的正弦值和余弦值，然后結合內角和定理，運用求解得到。
解: （1）f(x)=cos(2x+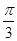)+sinx.=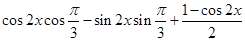
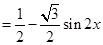           所以函數f(x)的最大值為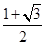,最小正周期.
（2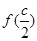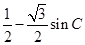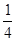）==－, 所以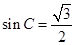, 因為C為銳角, 所以,
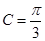又因為在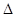ABC 中,  cosB=,  所以 ,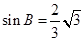
所以
考點：本試題主要考查了三角函數的圖像與性質的運用。
點評：解決該試題的關鍵是將函數化為單一函數，結合三角函數的性質得到其最值和周期，統統是結合三角形中同角關系式和兩角和差的公式能得到解三角形。

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：解答題

在中，．
（1）求角的大小；
（2）若，，求．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

在中，角所對的邊分別為,設為的面積，滿足.
（Ⅰ）求角的大小；
（Ⅱ）求的最大值.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

（本題滿分13 分）
據氣象部門預報，在距離某碼頭南偏東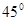方向600km處的熱帶風暴中心，正以每小時20km的速度向正北方向移動，距風暴中心450km以內的地區都將受到影響，從現在起多長時間后，該碼頭將受到熱帶風暴中心的影響，影響多長時間？（精確到0.1h）

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

（本小題12分）在△ABC中，內角的對邊分別為，且
（Ⅰ）求角的大小；
（II）若求的值.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

（本題滿分13分）我炮兵陣地位于地面A處，兩觀察所分別位于地面點C和D處，已知CD=6，∠ACD=45°,∠ADC=75°, 目標出現于地面點B處時，測得∠BCD=30°，∠BDC=15°(如圖），求炮兵陣地到目標的距離.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

（本題12分）已知分別為三個內角的對邊，，（1）求；  （2）若，的面積為；求.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

如圖，在中, .
（1）求sinA
（2）記BC的中點為D，求中線AD的長.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

(本題滿分14分)在銳角三角形ABC中，已知角A、B、C所對的邊分別為a、b、c，且，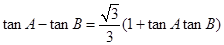
（1）若c2＝a2＋b2—ab，求角A、B、C的大小；
（2）已知向量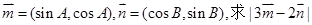的取值范圍。

查看答案和解析>>

同步練習冊答案