
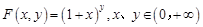 .
.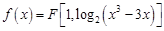 與直線
與直線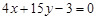 垂直的切線方程;
垂直的切線方程;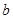 使曲線
使曲線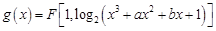 在
在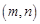 點處的切線斜率為
點處的切線斜率為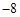 ,且
,且 ,求實數
,求實數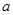 的取值范圍.
的取值范圍.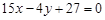 . (2)
. (2)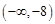 。
。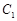 的切線與直線
的切線與直線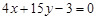 垂直,故令
垂直,故令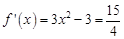 得
得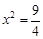 得到
得到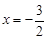 ,進而得到切線方程。
,進而得到切線方程。
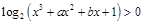 ,得
,得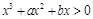
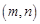 ,故有
,故有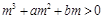 ,構造函數利用導數求解不等式轉化為
,構造函數利用導數求解不等式轉化為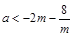 在
在 上有解來解決。
上有解來解決。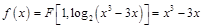 ,
, 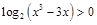 ①, -------------------------2分
①, -------------------------2分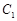 的切線與直線
的切線與直線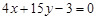 垂直,故令
垂直,故令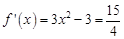 得
得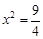 ②,由①②知應取
②,由①②知應取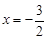 ,得
,得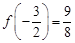 ,切點為
,切點為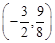 ,
,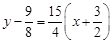 ,即
,即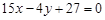 .------------------4分
.------------------4分
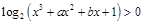 ,得
,得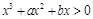
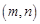 ,故有
,故有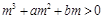 -----------------6分
-----------------6分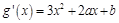 ,依題意有
,依題意有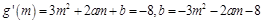
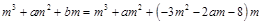
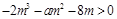 ---------------------8分
---------------------8分 上有解,即
上有解,即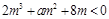 在
在 上有解,
上有解, 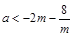 在
在 上有解,-------- -------------10分
上有解,-------- -------------10分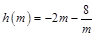 ,則
,則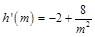 ,在
,在 上恒有
上恒有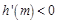
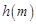 是
是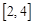 上的減函數,
上的減函數,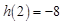 ,所以實數
,所以實數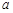 的取值范圍是
的取值范圍是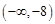 --------------12分
--------------12分

 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:高中數學 來源:不詳 題型:解答題
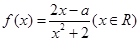
 時,求曲線
時,求曲線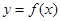 在點
在點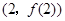 處的切線方程;
處的切線方程;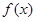 在區間
在區間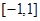 上是增函數,求實數
上是增函數,求實數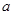 的取值范圍
的取值范圍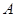 ;
;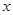 的方程
的方程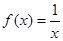 的兩個根為
的兩個根為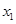 、
、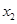 ,若對任意
,若對任意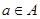 ,
,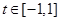 ,不等式
,不等式 恒成立,求
恒成立,求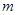 的取值范圍.
的取值范圍. 查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
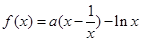
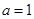 時,求曲線
時,求曲線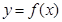 在點
在點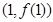 處的切線方程;
處的切線方程;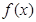 在其定義域內為增函數,求實數
在其定義域內為增函數,求實數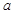 的取值范圍;
的取值范圍;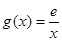 ,若在
,若在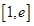 上至少存在一點
上至少存在一點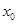 使
使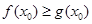 成立,求實數
成立,求實數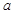 的取值范圍.
的取值范圍.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com