
已知函數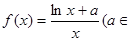 R).
R).
(1)若曲線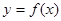 在點
在點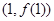 處的切線與直線
處的切線與直線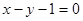 平行,求
平行,求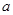 的值;
的值;
(2)在(1)條件下,求函數 的單調區間和極值;
的單調區間和極值;
(3)當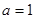 ,且
,且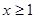 時,證明:
時,證明: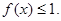
(1)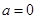 ;(2)詳見解析.
;(2)詳見解析.
解析試題分析:(1)欲求a的值,根據在點(1,f(1))處的切線方程,只須求出其斜率的值即可,故先利用導數求出在x=1處的導函數值,再結合導數的幾何意義即可求出切線的斜率.再列出一個等式,最后解方程組即可得.
(2)先求出f(x)的導數,根據f′(x)>0求得的區間是單調增區間,f′(x)<0求得的區間是單調減區間,最后求出極值即可.
(3)由(2)知,當a=1時,函數f(x)=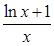 ,在[1,+∞)上是單調減函數,且f(1)=
,在[1,+∞)上是單調減函數,且f(1)=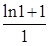 =1,從而證得結論..
=1,從而證得結論..
試題解析:解:(1)函數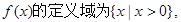
所以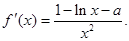 又曲線
又曲線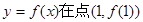 處的切線與直線
處的切線與直線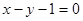 平行,所以
平行,所以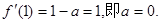 4分;
4分;
(2)令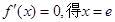
當x變化時,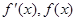 的變化情況如下表:
的變化情況如下表:
由表可知:
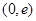
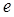
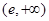
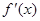
+ 0 — 

極大值 
 的單調遞增區間是
的單調遞增區間是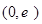 ,單調遞減區間是
,單調遞減區間是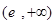
所以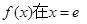 處取得極大值,
處取得極大值,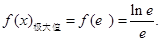 8分;
8分;
(3)當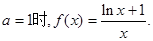 由于
由于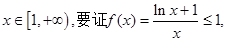
只需證明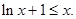
令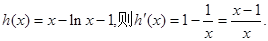
因為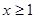 ,所以
,所以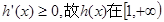 上單調遞增,
上單調遞增,
當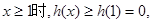 即
即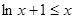 成立。
成立。
故當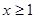 時,有
時,有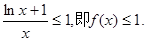 12分;
12分;
考點:1.利用導數研究函數的極值;2.利用導數研究函數的單調性;3.利用導數研究曲線上某點切線方程.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
某工廠有一批貨物由海上從甲地運往乙地,已知輪船的最大航行速度為60海里/小時,甲地至乙地之間的海上航行距離為600海里,每小時的運輸成本由燃料費和其他費用組成,輪船每小時的燃料費與輪船速度的平方成正比,比例系數為0.5,其余費用為每小時1250元。
(1)把全程運輸成本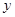 (元)表示為速度
(元)表示為速度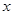 (海里/小時)的函數;
(海里/小時)的函數;
(2)為使全程運輸成本最小,輪船應以多大速度行駛?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,半徑為30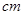 的圓形(
的圓形( 為圓心)鐵皮上截取一塊矩形材料
為圓心)鐵皮上截取一塊矩形材料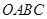 ,其中點
,其中點 在圓弧上,點
在圓弧上,點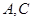 在兩半徑上,現將此矩形材料卷成一個以
在兩半徑上,現將此矩形材料卷成一個以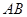 為母線的圓柱形罐子的側面(不計剪裁和拼接損耗),設
為母線的圓柱形罐子的側面(不計剪裁和拼接損耗),設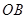 與矩形材料的邊
與矩形材料的邊 的夾角為
的夾角為 ,圓柱的體積為
,圓柱的體積為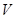
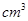 .
.
(1)求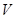 關于
關于 的函數關系式?
的函數關系式?
(2)求圓柱形罐子體積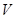 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com