
��ֱ������ƽ���(n��i)��y�S�҂�(c��)��һ���cP���c �ľ��x������
�ľ��x������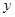 �S�ľ��x��
�S�ľ��x��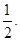
��������c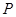 ��܉�E
��܉�E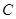 �ķ��̣�
�ķ��̣�
�����O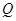 ������
������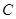 �ϵ�һ�����c���c
�ϵ�һ�����c���c ��
��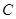 ��
��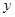 �S�ϣ���
�S�ϣ���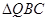 ��A
��A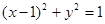 ��������������
�����������Σ���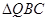 ��e����Сֵ.
��e����Сֵ.
���� ����8.
����8.
����ԇ�}����������ͨ�^׃�Q�ͷ����ɵ��c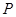 ��܉�E�ǒ��タ�����ö��x������˜ʷ��̣�����������e��С��������e���_ʽ.
��܉�E�ǒ��タ�����ö��x������˜ʷ��̣�����������e��С��������e���_ʽ.
ԇ�}�������������}֪�c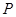 ��
�� �ľ��x�c����ֱ��
�ľ��x�c����ֱ��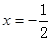 �ľ��x��ȣ�
�ľ��x��ȣ�
�����c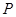 ��܉�E�ǒ��タ�����̞�
��܉�E�ǒ��タ�����̞� 4��
4��
�����O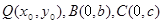 ���t
���t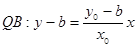 ��
��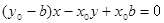
��ֱ��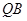 �LjA���о�֪
�LjA���о�֪ ��
��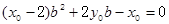
ͬ����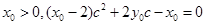 ����
���� �Ƿ���
�Ƿ��� �ăɸ�
�ăɸ�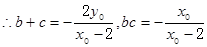 8��
8��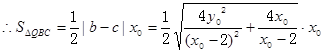
��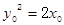
 ���}֪
���}֪
 ��
��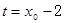
�t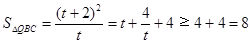 ��
�� ��
�� �r��ȡ��
�r��ȡ��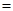 ��
�� ��e����Сֵ��
��e����Сֵ�� 12��
12��
���c����������܉�E���̣������\�㣬��������ʽ.



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M�n�����]�� | ��һ | ��һ���M�n�����]�� |
| �߶� | �߶����M�n�����]�� | ���� | �������M�n�����]�� |
| ���� | �������M�n�����]�� | ���� | �������M�n�����]�� |
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�����}
��֪�E�A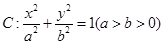 ���x���ʞ�
���x���ʞ�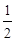 ����ԭ�c��A�ģ��E�A�Ķ̰��S��돽�ĈA�cֱ��
����ԭ�c��A�ģ��E�A�Ķ̰��S��돽�ĈA�cֱ��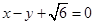 ���У�ֱ��
���У�ֱ��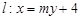 �c�E�AC�ཻ��A��B���c.
�c�E�AC�ཻ��A��B���c.
��1����E�AC�ķ��̣���2����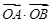 ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�����}
��֪�E�A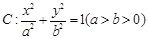 ���x���ʞ�
���x���ʞ�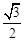 ���ҽ�(j��ng)�^�c
���ҽ�(j��ng)�^�c ��
��
(��)��E�A�ķ��̣�
(��)����^�c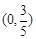 ��ֱ���c�E�A����
��ֱ���c�E�A���� ���c��
���c�� �c�c
�c�c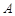 �c���غϣ���
�c���غϣ���
����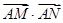 ��ֵ��
��ֵ��
�ڮ�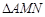 �����ֱ�������Εr����ֱ��
�����ֱ�������Εr����ֱ��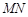 �ķ��̣�
�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�����}
��ƽ��ֱ������ϵ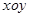 �У��c
���c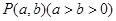 ����c��
����c��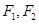 �քe��E�A
�քe��E�A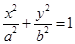 �����ҽ��c����֪��
�����ҽ��c����֪��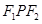 ����������Σ���1����E�A���x����
����������Σ���1����E�A���x����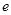 ����2���Oֱ��
����2���Oֱ��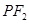 �c�E�A�ཻ��
�c�E�A�ཻ��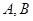 ���c��
���c��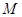 ��ֱ��
��ֱ��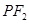 �ϵ��c���M��
�ϵ��c���M��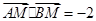 �����c
�����c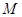 ��܉�E���̣�
��܉�E���̣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�����}
��֪��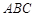 �ăɂ���c
�ăɂ���c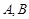 �����˷քe��
�����˷քe��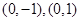 ����
����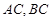 ����ֱ����б��֮�e����
����ֱ����б��֮�e����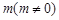 ��
��
��������c ��܉�E
��܉�E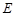 �ķ��̣����Д�܉�E
�ķ��̣����Д�܉�E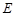 ��ηN�A�F������
��ηN�A�F������
����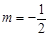 �r���^�c
�r���^�c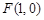 ��ֱ��
��ֱ��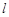 ������
������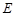 ��
�� ���c���O�c
���c���O�c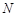 �P(gu��n)��
�P(gu��n)�� �S���Q
�S���Q
�c��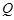 (
(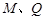 ���غ�) ԇ����ֱ��
���غ�) ԇ����ֱ��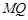 �c
�c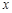 �S�Ľ��c�Ƿ��Ƕ��c�����ǣ�������c�������ǣ�Ո�f������.
�S�Ľ��c�Ƿ��Ƕ��c�����ǣ�������c�������ǣ�Ո�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�����}
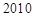 ��
��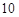 ��
��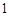 ��
��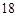 �r
�r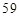 ��
�� �롰�϶��̖��̽���l(w��i)�����L����̖���\�d�����������c�߶ȼs
�롰�϶��̖��̽���l(w��i)�����L����̖���\�d�����������c�߶ȼs ����h���c�߶ȼs
����h���c�߶ȼs �f�����ֱ�ӱ��E�A(��������
�f�����ֱ�ӱ��E�A(�������� ��һ�����c)܉�����w�С����l(w��i)�ǵ��_�������ض�λ�Õr����ʩ�����ƄӼ�܉���{(di��o)�����l(w��i)��׃܉�M���h����
��һ�����c)܉�����w�С����l(w��i)�ǵ��_�������ض�λ�Õr����ʩ�����ƄӼ�܉���{(di��o)�����l(w��i)��׃܉�M���h���� ���������
��������� ����(��������
����(��������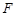 ��һ�����c)�ęE�A܉�����@���w�У�֮���l(w��i)���ٴΓ�C׃܉�M����
��һ�����c)�ęE�A܉�����@���w�У�֮���l(w��i)���ٴΓ�C׃܉�M����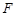 ��A�ġ�������
��A�ġ�������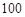 ����ĈA��܉�����@���w�У����_չ���P(gu��n)���g(sh��)ԇ�ͿƌW̽�y����֪����돽�s��
����ĈA��܉�����@���w�У����_չ���P(gu��n)���g(sh��)ԇ�ͿƌW̽�y����֪����돽�s��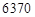 �������돽�s��
�������돽�s��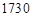 ���
���
�����^�E�A܉�����c�E�A܉������x���ʵĴ�С��
������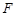 ���ҽ��c,��E�A܉����Ę˜ʷ��̡�
���ҽ��c,��E�A܉����Ę˜ʷ��̡�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�����}
��D��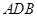 ���A��
���A�� ���Aֱ����
���Aֱ����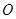 ���A�A�ģ���
���A�A�ģ���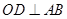 ��
��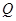 �龀��
�龀��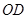 �����c����֪
�����c����֪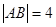 ������
������ �^
�^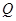 �c�����c
�c�����c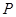 ������
������ ���\���ұ���
���\���ұ���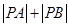 ��ֵ��׃.
��ֵ��׃.
(I)�����m��?sh��)�ƽ��ֱ������ϵ�������� �ķ��̣�
�ķ��̣�
(II)�^�c ��ֱ��
��ֱ�� �c����
�c���� ����
���� ���c���c
���c���c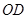 ����ֱ������
����ֱ������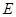 �c��
�c��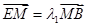 ��
��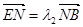 �C����
�C���� �鶨ֵ.
�鶨ֵ.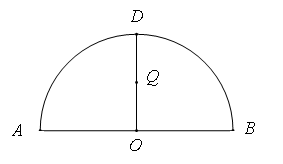
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�����}
��D��ʾ����֪�^���タ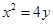 �Ľ��cF��ֱ��
�Ľ��cF��ֱ�� �c���タ�ཻ��A��B���c��
�c���タ�ཻ��A��B���c��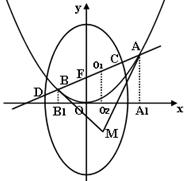
��1�����C����AF��ֱ���ĈA�cx�S���У�
��2���O���タ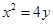 ��A��B���c̎���о��Ľ��c��M�����cM�ęM���˞�2�����ABM����ӈA���̣�
��A��B���c̎���о��Ľ��c��M�����cM�ęM���˞�2�����ABM����ӈA���̣�
��3���O�^���タ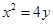 ���cF��ֱ��
���cF��ֱ�� �c�E�A
�c�E�A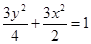 �Ľ��c��C��D���Ƿ����ֱ��
�Ľ��c��C��D���Ƿ����ֱ�� ʹ��
ʹ��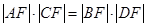 �������ڣ����ֱ��
�������ڣ����ֱ�� �ķ��̣��������ڣ�Ո�f�����ɡ�
�ķ��̣��������ڣ�Ո�f�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�����}
��֪�E�A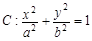 ��a��b��0���Ľ�����4�����c�E�A
��a��b��0���Ľ�����4�����c�E�A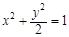 ����ͬ���x���ʣ�б�ʞ�k��ֱ��l��(j��ng)�^�cM��0��1�����c�E�AC���ڲ�ͬ���cA��B��
����ͬ���x���ʣ�б�ʞ�k��ֱ��l��(j��ng)�^�cM��0��1�����c�E�AC���ڲ�ͬ���cA��B��
��1����E�AC�Ę˜ʷ��̣�
��2�����E�AC���ҽ��cF����AB��ֱ���ĈA��(n��i)�r����k��ȡֵ������
�鿴�𰸺ͽ���>>
���H�WУ��(y��u)�x - �������б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com