
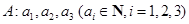 ,定義“
,定義“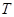 變換”:
變換”: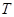 將數列
將數列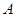 變換成數列
變換成數列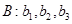 ,其中
,其中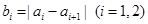 ,且
,且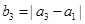 .這種“
.這種“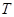 變換”記作
變換”記作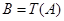 .繼續對數列
.繼續對數列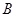 進行“
進行“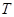 變換”,得到數列
變換”,得到數列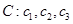 ,依此類推,當得到的數列各項均為
,依此類推,當得到的數列各項均為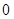 時變換結束.
時變換結束.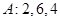 經過不斷的“
經過不斷的“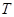 變換”能否結束?若能,請依次寫出經過“
變換”能否結束?若能,請依次寫出經過“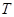 變換”得到的各數列;若不能,說明理由;
變換”得到的各數列;若不能,說明理由;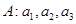 ,
,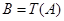 .若
.若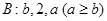 ,且
,且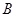 的各項之和為
的各項之和為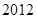 .
.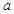 ,
,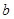 ;
;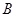 再經過
再經過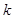 次“
次“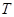 變換”得到的數列各項之和最小,求
變換”得到的數列各項之和最小,求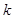 的最小值,并說明理由.
的最小值,并說明理由.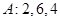 不能結束,各數列依次為
不能結束,各數列依次為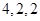 ;
;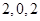 ;
;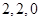 ;
;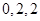 ;
;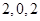 ;….
;….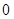 的情形. ………3分
的情形. ………3分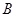 的各項之和為
的各項之和為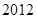 ,且
,且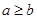 ,所以
,所以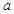 為
為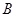 的最大項,
的最大項,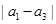 最大,即
最大,即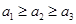 ,或
,或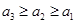 . …………5分
. …………5分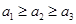 時,可得
時,可得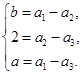
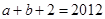 ,得
,得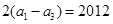 ,即
,即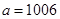 ,故
,故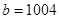 .…7分
.…7分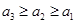 時,同理可得
時,同理可得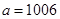 ,
,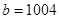 . ………8分
. ………8分 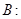
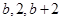 ,則
,則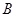 經過
經過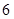 次“
次“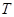 變換”得到的數列分別為:
變換”得到的數列分別為: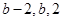 ;
;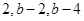 ;
;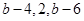 ;
;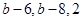 ;
;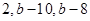 ;
;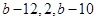 .
.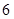 次“
次“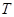 變換”后得到的數列也是形如“
變換”后得到的數列也是形如“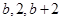 ”的數列,與數列
”的數列,與數列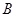 “結構”完全相同,但最大項減少12.
“結構”完全相同,但最大項減少12. ,
,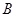 經過
經過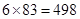 次“
次“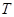 變換”后得到的數列為
變換”后得到的數列為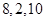 .
.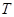 變換”后得到的數列分別為:
變換”后得到的數列分別為: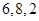 ;
;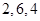 ;
;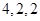 ;
;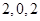 ;
;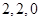 ;
;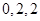 ;
;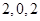 ,……
,……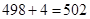 次“
次“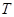 變換”得到的數列各項和最小,
變換”得到的數列各項和最小,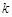 的最小值為
的最小值為 .
.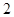 ,較大兩項相差
,較大兩項相差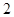 ,則稱此數列與數列
,則稱此數列與數列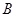 “結構相同”.
“結構相同”.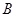 的三項為
的三項為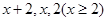 ,則無論其順序如何,經過“
,則無論其順序如何,經過“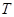 變換”得到的數列的三項為
變換”得到的數列的三項為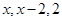 (不考慮順序) .
(不考慮順序) .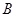 結構相同的數列經過“
結構相同的數列經過“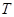 變換”得到的數列也與
變換”得到的數列也與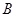 結構相同,除
結構相同,除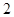 外其余各項減少
外其余各項減少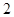 ,各項和減少
,各項和減少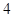 .
.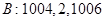 經過
經過 次“
次“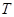 變換”一定得到各項為
變換”一定得到各項為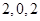 (不考慮順序)的數列.
(不考慮順序)的數列.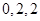 的數列,無論順序如何,經過“
的數列,無論順序如何,經過“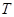 變換”得到的數列會重復出現,各項和不再減少.
變換”得到的數列會重復出現,各項和不再減少. 次“
次“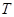 變換”,得到的數列各項和最小,故
變換”,得到的數列各項和最小,故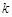 的最小值為
的最小值為 .
.

科目:高中數學 來源:不詳 題型:單選題
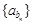 的前10項的和等于
的前10項的和等于| A.55 | B.70 |
| C.85 | D.100 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com