
已知函數 ,其圖象在點
,其圖象在點 處的切線方程為
處的切線方程為
(1)求 的值;
的值;
(2)求函數 的單調區間,并求出
的單調區間,并求出 在區間[-2,4]上的最大值.
在區間[-2,4]上的最大值.
(1) a=1,b=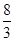 . (2)8.
. (2)8.
解析試題分析:(1)f′(x)=x2-2ax+a2-1, 2分
∵(1,f(1))在x+y-3=0上,∴f(1)=2, 3分
∵(1,2)在y=f(x)的圖象上,∴2=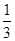 -a+a2-1+b,
-a+a2-1+b,
又f′(1)=-1,∴a2-2a+1=0,
解得a=1,b=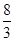 . 6分
. 6分
(2)∵f(x)=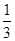 x3-x2+
x3-x2+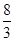 ,∴f′(x)=x2-2x,
,∴f′(x)=x2-2x,
由f′(x)=0可知x=0和x=2是f(x)的極值點,所以有
8分x (-∞,0) 0 (0,2) 2 (2,+∞) f′(x) + 0 - 0 + f(x) ? 極大值 ? 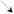
極小值 ? 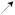
所以f(x)的單調遞增區間是(-∞,0)和(2,+∞),單調遞減區間是(0,2). 10分
∵f(0)=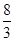 ,f(2)=
,f(2)=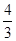 ,f(-2)=-4,f(4)=8,
,f(-2)=-4,f(4)=8,
∴在區間[-2,4]上的最大值為8. 13分
考點:導數的幾何意義;利用導數研究函數的單調性;利用導數研究函數的最值。
點評:我們要靈活應用導數的幾何意義求曲線的切線方程,尤其要注意切點這個特殊點,充分利用切點即在曲線方程上,又在切線方程上,切點處的導數等于切線的斜率這些條件列出方程組求解。屬于基礎題。


 課時訓練江蘇人民出版社系列答案
課時訓練江蘇人民出版社系列答案科目:高中數學 來源: 題型:解答題
(本小題14分)已知函數 ,設
,設 。
。
(Ⅰ)求F(x)的單調區間;
(Ⅱ)若以 圖象上任意一點
圖象上任意一點 為切點的切線的斜率
為切點的切線的斜率 恒成立,求實數
恒成立,求實數 的最小值。
的最小值。
(Ⅲ)是否存在實數 ,使得函數
,使得函數 的圖象與
的圖象與 的圖象恰好有四個不同的交點?若存在,求出
的圖象恰好有四個不同的交點?若存在,求出 的取值范圍,若不存在,說名理由。
的取值范圍,若不存在,說名理由。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
設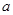 ∈R,函數
∈R,函數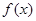 =
=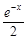 (
(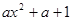 ),其中e是自然對數的底數.
),其中e是自然對數的底數.
(1)判斷f (x)在R上的單調性;
(2)當– 1 <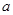 < 0時,求f (x)在[1,2]上的最小值.
< 0時,求f (x)在[1,2]上的最小值.
選做題:請考生從給出的3道題中任選一題做答,并在答題卡上把所選題目的題號用2B鉛筆涂黑.注意所做題目的題號必須與所涂的題號一致,在答題卡選答區域指定位置答題.如果多做,則按所做的第一題計分.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分14分)
若函數 對任意的實數
對任意的實數 ,
, ,均有
,均有 ,則稱函數
,則稱函數 是區間
是區間 上的“平緩函數”.
上的“平緩函數”.
(1) 判斷 和
和 是不是實數集R上的“平緩函數”,并說明理由;
是不是實數集R上的“平緩函數”,并說明理由;
(2) 若數列 對所有的正整數
對所有的正整數 都有
都有  ,設
,設 ,
,
求證:  .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com