
(本大題13分)設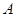 、
、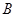 為函數
為函數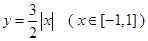 圖象上不同的兩個點,
圖象上不同的兩個點,
且 AB∥ 軸,又有定點
軸,又有定點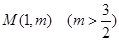 ,已知
,已知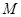 是線段
是線段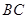 的中點.
的中點.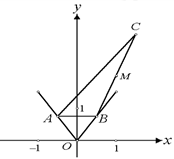
⑴ 設點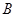 的橫坐標為
的橫坐標為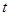 ,寫出
,寫出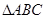 的面積
的面積 關于
關于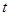 的函數
的函數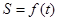 的表達式;
的表達式;
⑵ 求函數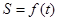 的最大值,并求此時點
的最大值,并求此時點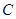 的坐標。
的坐標。
科目:高中數學 來源: 題型:解答題
某省兩相近重要城市之間人員交流頻繁,為了緩解交通壓力,特修一條專用鐵路,用一列火車作為交通車,已知該車每次拖4節車廂,一日能來回16次, 如果每次拖7節車廂,則每日能來回10次.
(1)若每日來回的次數是車頭每次拖掛車廂節數的一次函數,求此一次函數解析式:
(2)在(1)的條件下,每節車廂能載乘客110人.問這列火車每天來回多少次才能使運營人數最多?并求出每天最多運營人數。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=x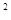 +2ax+2, x
+2ax+2, x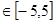 .
.
(1)當a=-1時,求函數的最大值和最小值;
(2) 若y=f(x)在區間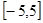 上是單調 函數,求實數 a的取值范圍.
上是單調 函數,求實數 a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某服裝廠生產一種服裝,每件服裝的成本為40元,出廠單價定為60元,該廠為鼓勵銷售商訂購,決定當一次訂購量超過100件時,每多訂購一件,訂購的全部服裝的出場單價就降低0.02元,根據市場調查,銷售商一次訂購量不會超過600件.
(1)設一次訂購x件,服裝的實際出廠單價為p元,寫出函數p=f(x)的表達式;
(2)當銷售商一次訂購多少件服裝時,該廠獲得的利潤最大?其最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某沿海地區養殖的一種特色海鮮上市時間僅能持續5個月,預測上市初期和后期會因供應不足使價格呈持續上漲態勢,而中期又將出現供大于求使價格連續下跌.現有三種價格模擬函數:①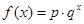 ;②
;②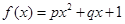 ;③
;③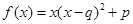 .(以上三式中、
.(以上三式中、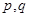 均為常數,且
均為常數,且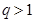 )
)
(I)為準確研究其價格走勢,應選哪種價格模擬函數(不必說明理由)
(II)若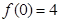 ,
,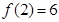 ,求出所選函數
,求出所選函數 的解析式(注:函數定義域是
的解析式(注:函數定義域是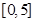 .其中
.其中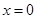 表示8月1日,
表示8月1日,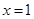 表示9月1日,…,以此類推);
表示9月1日,…,以此類推);
(III)在(II)的條件下研究下面課題:為保證養殖戶的經濟效益,當地政府計劃在價格下跌期間積極拓寬外銷,請你預測該海鮮將在哪幾個月份內價格下跌.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了保護水資源,提倡節約用水,某市對居民生活用水收費標準如下:每戶每月用水不超過6噸時每噸3元,當用水超過6噸但不超過15噸時,超過部分每噸5元,當用水超過15噸時,超過部分每噸10元。
(1)求水費y(元)關于用水量x(噸)之間的函數關系式;
(2)若某戶居民某月所交水費為93元,試求此用戶該月的用水量。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
函數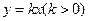 的圖象與函數
的圖象與函數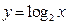 的圖象交于兩點
的圖象交于兩點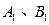 (
(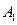 在線段
在線段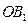 上,
上,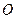 為坐標原點),過
為坐標原點),過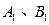 作
作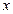 軸的垂線,垂足分別為
軸的垂線,垂足分別為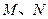 ,并且
,并且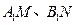 分別交函數
分別交函數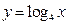 的圖象于
的圖象于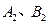 兩點.
兩點.
(1)試探究線段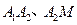 的大小關系;
的大小關系;
(2)若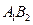 平行于
平行于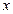 軸,求四邊形
軸,求四邊形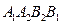 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分12分)有甲、乙兩種商品,經營銷售這兩種商品所能獲得的利潤依次是P和Q(萬元),它們與投入資金x(萬元)的關系有經驗公式:P=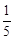 x,Q=
x,Q=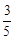
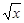 .今有3萬元資金投入經營甲、乙兩種商品,為獲得最大利潤,對甲、乙兩種商品的資金投入分別應為多少,能獲得的最大利潤為多少?
.今有3萬元資金投入經營甲、乙兩種商品,為獲得最大利潤,對甲、乙兩種商品的資金投入分別應為多少,能獲得的最大利潤為多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com