
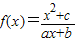 為奇函數,f(1)<f(3),且不等式
為奇函數,f(1)<f(3),且不等式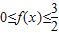 的解集是[-2,-1]∪[2,4]
的解集是[-2,-1]∪[2,4]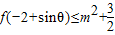 對一切θ∈R成立?若存在,求出m的取值范圍;若不存在,請說明理由.
對一切θ∈R成立?若存在,求出m的取值范圍;若不存在,請說明理由.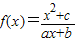 為奇函數,則f(-x)=-f(x),構造方程可得b值,由不等式
為奇函數,則f(-x)=-f(x),構造方程可得b值,由不等式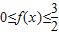 的解集是[-2,-1]∪[2,4],根據±2均為不等式的解,可得c值,根據f(1)<f(3),結合函數單調性,及不等式解集的端點是對應方程的根,求出a值.
的解集是[-2,-1]∪[2,4],根據±2均為不等式的解,可得c值,根據f(1)<f(3),結合函數單調性,及不等式解集的端點是對應方程的根,求出a值. ,
,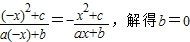 .…(1分)
.…(1分)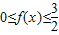 的解集中包含2和-2,
的解集中包含2和-2,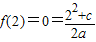 ,所以c=-4…(2分)
,所以c=-4…(2分)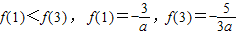 ,
,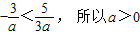 .…(3分)
.…(3分)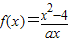 是增函數
是增函數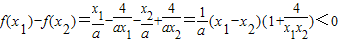
 …(5分)
…(5分)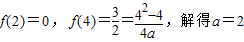 .
.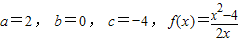 …(6分)
…(6分)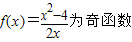 ,
,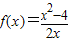 在(-∞,0)上也是增函數.…(7分)
在(-∞,0)上也是增函數.…(7分)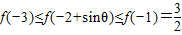 ,
,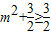 ,
,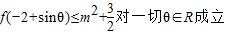 …(12分)
…(12分)

 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案科目:高中數學 來源: 題型:解答題
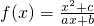 為奇函數,f(1)=-3,且對任意x∈[π,2π],f(sinx-1)≥0恒成立,f(cosx+3)≥0恒成立.
為奇函數,f(1)=-3,且對任意x∈[π,2π],f(sinx-1)≥0恒成立,f(cosx+3)≥0恒成立.查看答案和解析>>
科目:高中數學 來源:山東省月考題 題型:解答題
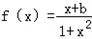 為奇函數.
為奇函數.查看答案和解析>>
科目:高中數學 來源:2012-2013學年山東省泰安市新泰市新汶中學高三(上)9月月考數學試卷(理科)(解析版) 題型:解答題
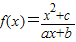 為奇函數,f(1)<f(3),且不等式
為奇函數,f(1)<f(3),且不等式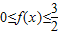 的解集是[-2,-1]∪[2,4]
的解集是[-2,-1]∪[2,4]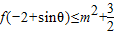 對一切θ∈R成立?若存在,求出m的取值范圍;若不存在,請說明理由.
對一切θ∈R成立?若存在,求出m的取值范圍;若不存在,請說明理由.查看答案和解析>>
科目:高中數學 來源:2010-2011學年黑龍江省哈爾濱市哈九中高一(上)期末數學試卷(解析版) 題型:解答題
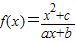 為奇函數,f(1)=-3,且對任意x∈[π,2π],f(sinx-1)≥0恒成立,f(cosx+3)≥0恒成立.
為奇函數,f(1)=-3,且對任意x∈[π,2π],f(sinx-1)≥0恒成立,f(cosx+3)≥0恒成立.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com