
已知 .
.
(1)求 的最小值及取最小值時
的最小值及取最小值時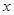 的集合;
的集合;
(2)求 在
在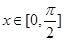 時的值域;
時的值域;
(3)在給出的直角坐標系中,請畫出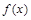 在區間
在區間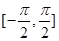 上的圖像(要求列表,描點).
上的圖像(要求列表,描點).
(1)當 ,
,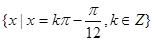 ;(2)
;(2)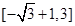 ;(3)詳見解析.
;(3)詳見解析.
解析試題分析:先根據平方差公式、同角三角函數的基本關系式、二倍角公式化簡所給的函數
科目:高中數學
來源:
題型:解答題
已知函數
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區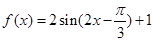 .(1)將
.(1)將 看成整體,然后由正弦函數
看成整體,然后由正弦函數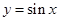 的最值可確定函數
的最值可確定函數 的最小值,并明確此時
的最小值,并明確此時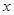 的值的集合;(2)先求出
的值的集合;(2)先求出 的范圍為
的范圍為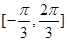 ,從而
,從而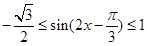 ,然后可求出
,然后可求出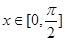 時,函數
時,函數 的值域;(3)根據正弦函數的五點作圖法進行列表、描點、連線完成作圖.
的值域;(3)根據正弦函數的五點作圖法進行列表、描點、連線完成作圖.
試題解析:化簡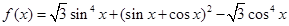
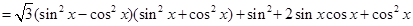
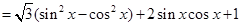
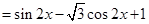
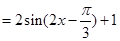 4分
4分
(1)當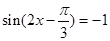 時,
時, 取得最小值
取得最小值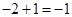 ,此時
,此時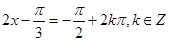 即
即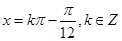 ,故此時
,故此時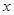 的集合為
的集合為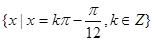 6分
6分
(2)當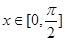 時,所以
時,所以 ,所以
,所以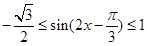 ,從而
,從而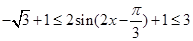 即
即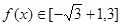 9分
9分
(3)由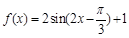 知
知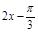
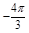
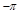
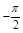
0 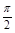
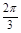
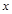
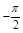
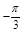
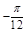
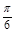

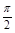
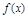




名題教輔暑假作業快樂生活武漢出版社系列答案
南粵學典名師金典測試卷系列答案
高分計劃小考必備升學全真模擬卷系列答案
金3練課堂作業實驗提高訓練系列答案
學與練期末沖刺奪100分系列答案
名校調研系列卷期末小綜合系列答案
黃岡狀元成才路應用題系列答案
小學畢業升學全真模擬卷內蒙古人民出版社系列答案
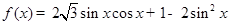 ,xÎR.
,xÎR.
(1)求函數 的最小正周期和單調遞增區間;
的最小正周期和單調遞增區間;
(2)將函數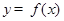 的圖象上各點的縱坐標保持不變,橫坐標先縮短到原來的
的圖象上各點的縱坐標保持不變,橫坐標先縮短到原來的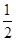 ,把所得到的圖象再向左平移
,把所得到的圖象再向左平移 單位,得到函數
單位,得到函數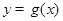 的圖象,求函數
的圖象,求函數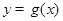 在區間
在區間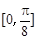 上的最小值.
上的最小值.
版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號