中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

（本小題滿分14分）
當均為正數(shù)時，稱為的“均倒數(shù)”．已知數(shù)列的各項均為正數(shù)，且其前項的“均倒數(shù)”為．
（1）求數(shù)列的通項公式；
（2）設，試比較與的大小；
（3）設函數(shù)，是否存在最大的實數(shù)，使當時，對于一切正整數(shù)，都有恒成立？
解：（1） ，
，兩式相減，得.
又，解得 ，∴….…4分                            
（2）∵，， 
∴， 即.   ……………………8分
（3）由（2）知數(shù)列 是單調(diào)遞增數(shù)列,是其的最小項，
即．……………………………………………………………9分
假設存在最大實數(shù),使當時,對于一切正整數(shù)，
都有 恒成立，……………………11分
則 ．只需， ………12分
即．解之得 或 ．
于是，可取  ………………………………………………………14分
略
練習冊系列答案
相關習題

科目：高中數(shù)學 來源：不詳 題型：解答題

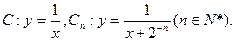（本小題滿分14分）已知曲線從C上一點Qn（xn，yn）作x軸的垂線，交Cn于點Pn，再從點Pn作y軸的垂線，交C于點Qn+1（xn+1，yn+1）。設x1＝1，an＝xn+1－xn，bn＝y(tǒng)n－yn+1     
①求Q1，Q2的坐標 ；②求數(shù)列{an}的通項公式；
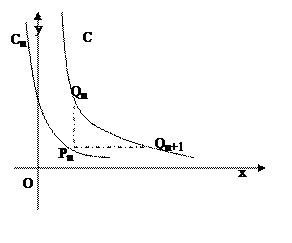③記數(shù)列{an·bn}的前n項和為Sn，求證：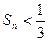

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：解答題

（本小題滿分12分）已知等差數(shù)列{}的前n項和為，且。
（1）求數(shù)列{}的通項公式；
（2）設，求數(shù)列{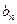}的前n項和。

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：單選題

等差數(shù)列滿足為常數(shù)，則其前（    ）項的和也是常數(shù)。
A．8B．9C．10D．11

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：單選題

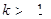預測人口的變化趨勢有很多方法，“直接推算法”使用的公式是其中為預測期內(nèi)年增長率，，為預測期人口數(shù)，為初期人口數(shù)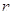，為預測期間隔年數(shù)。如果在某一時期有，那么在這期間人口數(shù)
A．擺動變化B．呈上升趨勢C．呈下降趨勢D．不變

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：解答題

（本小題滿分12分）已知數(shù)列{an}滿足   a1＝1,an＋1＝.,寫出它的前5項,并歸納出數(shù)列的一個通項公式(不要求證明)

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：解答題

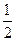(本題滿分16分)A、B是函數(shù)f(x)=+的圖象上的任意兩點，且=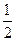()，已知點M的橫坐標為.
(Ⅰ)求證：M點的縱坐標為定值；
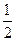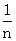(Ⅱ)若Sn=f()+f()+…+f()，n∈N+且n≥2，求Sn；
(Ⅲ)已知數(shù)列{an}的通項公式為. Tn為其前n項的和，若Tn<(Sn+1+1)，對一切正整數(shù)都成立，求實數(shù)的取值范圍.

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：單選題

已知方程的四個實根組成以為首項的等差數(shù)列,則
A.2               C.      D.

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：填空題

在等差數(shù)列中，前5項和則其公差          

查看答案和解析>>

同步練習冊答案